Uma mãe australiana lançou o alvoroço quando publicou o trabalho de casa da filha de 11 anos na Internet. Era uma questão de matemática que as duas só conseguiram resolver ao fim de 45 minutos e que envolvia números e cinco incógnitas difíceis de desvendar. “O meu cérebro está frito e até se costuma dizer que este é o ano mais fácil da escola”, confessou a mãe, que trabalha na área de administração de empresas, a um jornal local.
O exercício perguntava o seguinte: “O Bob soma duas fracções, mas não usa o mínimo denominador comum. Complete os espaços em branco”. A seguir, uma série de fracções, pontos de interrogações, somas e igualdades que foram o pesadelo da família australiana. O trabalho de casa era assim:
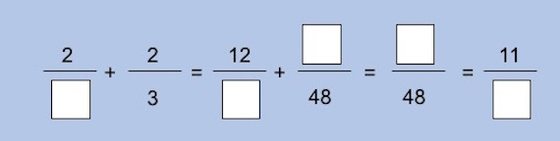
Entende agora a complicação? Aqui no Observador já temos as respostas, mas não podíamos deixar de lançar o desafio aos nossos leitores. Trocado por miúdos: é preciso descobrir que números completam corretamente os cinco quadrados, mas não se podem usar as técnicas típicas para tal — através do denominador e do numerador comuns. Estamos perante mais um exercício de raciocínio que demorou 45 minutos a resolver por esta mãe. Consegue resolver em menos?
Tire algum tempo para arranjar uma estratégia para este trabalho de casa para crianças de 11 anos (sem pressão!). Aqui em baixo propomos uma forma de resolver o problema. Bom trabalho!
…
…
…
…
…
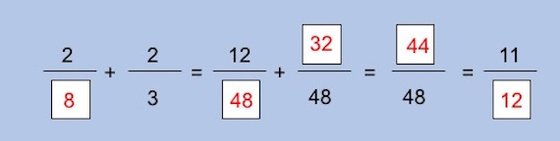
Bem-vindo de volta! Arranjou solução? Caso não tenha conseguido resolver este trabalho de casa, não desespere: é aqui que vai encontrar tudo o que precisa de saber para preencher corretamente os espaços em branco. Uma boa técnica para começar a organizar a mente é chamar os nomes pelos bois ou, como se diz em matemática, atribuir letras a cada um dos espaços que não sabemos quais são: as incógnitas. Sendo assim, as fracções ganham o seguinte aspeto (com as incógnitas marcadas a vermelho):

Agora vamos por partes. Comecemos pela igualdade que relaciona a incógnita “y”, “z” e “a”. Podemos reparar que o valor dado a “y” tem de permitir que a soma com a outra fracção, cujo denominador é 48, resulta numa outra fracção também com denominador 48. Ora, de acordo com as regras matemáticas, os denominadores de duas fracções não se somam. Se a soma de duas fracções tem de resultar numa fracção com denominador 48 e uma delas já tem esse denominador também, então o valor de “y” só pode ser também 48.
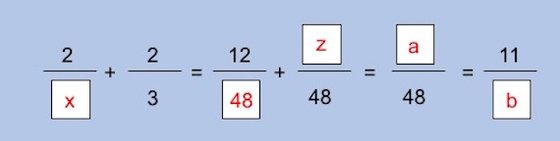
Próximo passo: a primeira igualdade de todas, entre as quatro primeiras fracções do problema em que as incógnitas são “x” e “z”. Se há duas fracções de cada lado da igualdade isso significa que cada uma das fracções equivale a outra que está do outro lado do igual. Como 2/3 não é igual a 12/48, então só pode ser igual a z/ 48. Obtemos então que 2/3 = z/48. Assim basta fazer a chamada regra de três simples: para descobrir o valor de “z” multiplica-se 2 por 48 (2×48) e divide-se o resultado dessa multiplicação por 3 (96÷3). Então, “z” é igual a 32.
Pela mesma ordem de ideias podemos descobrir o valor de “x”. Como 2/3 equivale à fracção onde antes estava a incógnita de “z”, então é porque a fracção 2/x corresponde à fracção 12/48. Obtemos então que 2/x = 12/48 e mais uma vez basta seguir a regra de três simples: para descobrir o valor de “x” multiplica-se 48 por 2 (48×2) e depois divide-se o resultado dessa multiplicação por 12 (96÷12). Sendo assim, “x” é igual a 8. E o exercício ganha um novo aspeto:
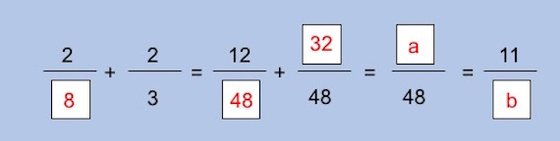
Falta agora descobrir os valores de “a” e de “b”. O valor de “a” é muito fácil de descobrir: como todas as fracções têm denominadores iguais, o valor de “a” pode ser obtido simplesmente somando os numeradores das fracções. Sendo assim, “a” é igual à soma de 12 com 32 (12+32), que é 44. Mais um avanço no exercício:
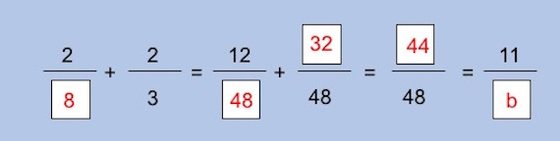
Agora, com uma única incógnita para resolver, basta fazer mais uma regra de três simples: para descobrir o valor de “b” basta multiplicar 48 por 11 (48×11) e depois dividir o resultado por 44 (528÷44). Então, o valor de “b” é 12. Temos agora tudo resolvido: x = 8, y = 48, z = 32, a = 44 e b = 12. Ainda acha difícil?