Parecia uma página de papel arrancada de um teste de matemática. Quem a partilhava pelas redes sociais fora dizia que era um exercício para crianças entre os cinco e os sete anos apresentado nas escolas de Singapura, que parecia não estar ao alcance da inteligência dos adultos. Mas não é verdade: na coluna “Can you Solve It” do The Guardian, Alex Bellos esclarece que esta história é um embuste e que o problema de matemática tem outra origem. Foi criado por Gordon Burgin, um professor reformado norte-americano que tem um blog recheado de desafios. Mas uma coisa está certa: as crianças têm mais facilidade em entendê-lo do que os adultos.
Para compreender o desafio é preciso ler com atenção o enunciado, que diz o seguinte:
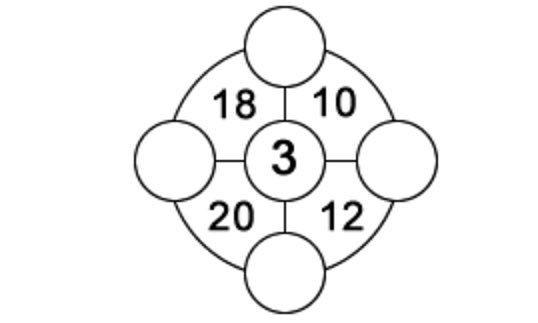
“Em cada uma das quatro secções do círculo mais exterior, há um número de dois dígitos que é igual à soma dos três números nos cantos do seu sector. Os números nos círculos individuais só podem estar entre 1 e 9 e cada número só pode ser usado uma vez. Um número já foi dado para início. Descubra os outros quatro”.
Veja aqui em baixo a imagem a que se refere o enunciado.
Está na hora de fazer contas — sim, desta vez precisamos de fazer contas, embora a máquina calculadora seja dispensável. Veja mais aqui em baixo as respostas finais ao exercício.
…
…
…
Bem-vindo de volta! Para entender o exercício que lhe propusemos é preciso dedicar-se a umas quantas equações. O primeiro conselho que lhe damos é a dar nomes a cada uma das bolas vazias, que são as incógnitas. De cima para baixo, e no sentido contrário ao ponteiro dos relógios, vamos chamar às bolas A, B, C e D tal como mostra a imagem seguinte.
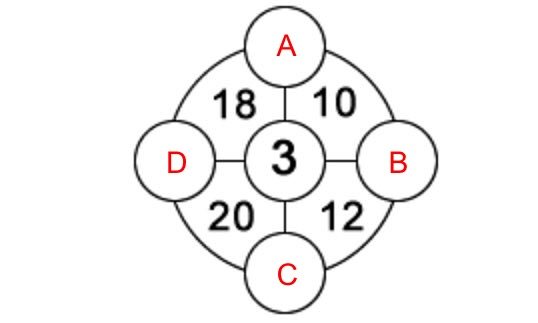
Sabemos que o valor de cada um dos setores do círculo equivale a soma do valor das duas letras a ele referentes mais 3, que é o valor indicado no círculo central. Esse vai ser o nosso ponto de partida porque nos fornece os cálculos de que precisamos. Desse modo, concluímos que:
- A + B + 3 = 10
- B + C + 3 = 12
- C + D + 3 = 20
- D + A + 3 = 18
Tendo isto em conta, podemos simplicar estes valores. Como? Arrumando a casa: do lado esquerdo do sinal de igual deixamos os valores que não conhecemos, ou seja, as letras; enquanto do lado direito do sinal de igual colocamos todos os valores que conhecemos, ou seja, os números. Para tal, basta passar o 3 para o lado contrário, algo que, segundo as regras básicas da matemática, existe que lhe troquemos o sinal. Obtemos então que:
- A + B = 10 – 3
- B + C = 12 – 3
- C + D = 20 – 3
- D + A = 18 – 3
Agora, basta fazer a subtração indicada do lado direito do sinal da igualdade. Isso significa que:
- A + B = 7
- B + C = 9
- C + D = 17
- D + A = 15
De acordo com o enunciado do problema, sabemos que os números correspondentes a cada um dos círculos está sempre compreendido entre 1 e 9, inclusive. Um truque para chegar mais rapidamente à solução é escrever cada um dos números das equações em cima como somas de dois números sempre maiores ou iguais a 1, mas também sempre iguais ou inferiores a 9. Sendo assim:
- A + B = (1 + 6) ou (2 + 5) ou (3 + 4). Ou seja, A e B podem cada um deles ter o valor de 1, 2, 3, 4 ou 5.
- B + C = (1 + 8) ou (2 + 7) ou (3 + 6) ou (4 + 5). Ou seja, B e C podem cada um deles ter o valor de 1, 2, 3, 4, 5, 6, 7 ou 8.
- C + D = (9 + 8). Ou seja, C e D podem cada um deles ter o valor de 8 ou 9.
- D + A = (9 + 6) ou (8 + 7). Ou seja, A e D podem cada um deles ter o valor de 6, 7, 8 ou 9.
Podemos perceber, olhando para as equações aqui em cima, que aquela que tem menos número de hipóteses é a correspondente a soma de C e D. É nele que vamos desenrolar este problema. Sabemos que D pode assumir o valor 9 ou de 8. Ora, como sabemos que A + D + 3 = 18, surgem aqui duas hipóteses:
- Se D = 8, então significa que A + 8 + 3 = 18. Simplificando a equação, descobrimos que A = 18 – 3 – 8 e, sendo assim, A = 7.
- Se D = 9, então significa que A + 9 + 3 = 18. Simplificando a equação, descobrimos que A = 18 – 3 – 9 e, sendo assim, A = 6.
Como é que tiramos as teimas? Se olharmos para a outra equação que envolve a letra A, que é A + B = 7, percebemos que A nunca pode ser igual 7 por dois motivos: primeiro, porque nas contas que fizemos lá em cima no ponto 1, o 7 não surge como um dos valores possíveis para A e B; e depois porque, se A fosse igual a 7, então B teria de ser igual a zero, algo que sabemos ser impossível porque o enunciado garante que todas as letras têm um valor entre 1 e 9.
Descobrimos assim que A = 6 e que D = 9.
Mas como é que descobrimos os valores de B e C? Para isso basta substituir, nas restantes equações, as letras A e D pelo valor a eles equivalente. Sendo assim:
- 6 + B = 7, então B = 1.
- 1 + C = 9, então C = 8.
- 8 + 9 = 17, como já sabíamos.
- 6 + 9 = 15, como já sabíamos.
Conclusão: A = 6, B = 1, C = 8 e D = 9.