Não é fácil, principalmente sem o apoio das máquinas de calcular. Mas há noventa finalistas das Olimpíadas das Matemáticas deste ano que conseguem responder a três destas dezasseis perguntas num máximo de três horas sem nada mais senão o próprio intelecto. Desde esta quarta-feira e até ao próximo domingo, a Sociedade Portuguesa de Matemática está na Escola Secundário Emídio de Navarro, em Viseu, à procura de prodígios das matemáticas. O nosso desafio era parecido: se resolvesse pelo menos três questões que lhe apresentámos neste artigo, talvez estivesse à altura de um deles. Mas será que conseguiu?

Agora que o relógio está prestes a parar, apresentamos-lhe aqui em baixo as soluções apresentadas pela Sociedade Portuguesa da Matemática para os enunciados das finais entre os anos letivos 2004/2005 e 2015/2016. É o veredicto: será que é um prodígio? Descubra aqui em baixo.

Um número de três algarismos diz-se firme se for igual ao produto do seu algarismo das unidades por um número formado pelos restantes algarismos. Por exemplo, 153 é firme porque 153 = 3 × 51. Quantos números firmes existem? Existem 688 números firmes.

• Seja N =100a + 10b + c. Se c(10a+b) = 100a + 10b +c = 10(10a+b)+c, entã c é múltiplo de 10a+b, o que é impossível.
• Então c(10b+a) = 100a + 10b + c, ou seja, c(10b+a−1) = 10(10a+b). Portanto, c= 5 ou 10b+a−1 é múltiplo de 5, ou seja, c = 5 ou a = 1 ou a = 6.
• Se c=5, então 5(10b+a−1) = 10(10a+b), ou seja, 8b = 19a + 1, o que é impossível com 0≤a, b≤9.
• Se a=1, então c(10b+1) = 100+10b+c, ou seja, b(c−1)=10. Obtemos as soluções b=2, c=6 e b = 5, c = 3, que correspondem aos números N = 126 e N = 153.
• Se a = 6, então c(10b+6) = 600+10b+c, ou seja, 2b(c−1) = 120−c. Obtemos as soluções b = 8,c = 8 que correspondem aos números N = 688.

O navio Meridiano do Bacalhau faz a sua campanha de pesca durante 64 dias. Em cada dia, o capitão escolhe um sentido de navegação, norte ou sul, e o barco navega nesse dia apenas nesse sentido. No primeiro dia da campanha o barco navega 1 milha, no segundo dia navega 2 milhas, e mais geralmente, no dia n navega n milhas. No final dos 64 dias, o barco estava a 2014 milhas a norte do ponto de partida da campanha. Qual é o número máximo de dias em que o navio pode ter navegado para sul? O navio navegou no máximo 7 dias para sul.

• O problema é equivalente ao de saber qual é o maior número de sinais “−” que se podem usar na igualdade ± 1 ± 2 ± 3 ± ··· ± 64 = 2014.
• Seja X o conjunto dos inteiros entre 1 e 64 que nessa igualdade ficam afetados com o sinal“−”.
• Ao subtrair ± 1 ± 2 ± 3 ± ··· ± 64 a 1 + 2 + 3 + ··· + 64, os números afetados com o sinal “+” cancelam, enquanto que os elementos de X dobram. Assim, se “s” for a soma dos elementos de X, então 1 + 2 + 3 + ··· + 64−2014 = 2s. Ora 1 + 2 + 3 + ··· + 64 = 64×65 = 2080, pelo que se tem 2s = 33 .
• Como 1 + 2 + 3 + · · · 7 + 8 = 8 × 9 = 36 > 33 , o número 33 não pode ser decomposto como uma soma soma de mais do que 7 elementos não repetidos de {1, . . . , 64}.
• Por outro lado, 33 admite a decomposição 1 + 2 + 3 + 4 + 5 + 6 + 12 = 33, pelo que se conclui que o número máximo de elementos que X pode ter é 7. Logo, o navio navegou no máximo de 7 dias para sul.

A Amélia e a Beatriz jogam à batalha naval num tabuleiro quadrado com 2n casas de lado, usando regras muito peculiares. O jogo começa com a Amélia a escolher n linhas e n colunas do tabuleiro, colocando em seguida os seus n² submarinos nas casas que ficam na sua interseção. De seguida, a Beatriz escolhe um conjunto de casas para torpedear. Qual é o número mínimo de casas que a Beatriz tem de escolher para ter a certeza de acertar em, pelo menos, um submarino? O número mínimo é 3n + 1 .

• Comecemos por provar que 3n não é suficiente. Mostremos que quaisquer que sejam as 3n casas que a Beatriz escolha, existe uma escolha da Amélia para a qual a Beatriz falha todos os “tiros”. Entre as 2n linhas do tabuleiro, escolhemos as n em que a Beatriz selecionou menos casas. No total estas linhas contêm no máximo n escolhas da Beatriz: se fossem mais, existiria uma linha no conjunto com mais de uma casa, enquanto como nas n linhas restantes estariam selecionadas menos de 2n casas alguma teria apenas uma, e não teríamos selecionado as linhas com menos casas atacadas.
• Mas então nestas n linhas, um máximo de n colunas contêm casas escolhidas pela Beatriz, ou seja, pelo menos n colunas não foram atacadas. Se a Amélia tivesse escolhido esta combinação de linhas e colunas então a Beatriz não teria acertado em nenhuma peça.
• Mostremos agora que 3n + 1 é suficiente. Consideremos as linhas e colunas indexadas de 1 a 2n, e admitamos que a Beatriz escolhe as 2n casas (1, 1), (2, 2), …, (2n, 2n), as n casas (1, 2), (2, 3), …, (n, n + 1) e ainda a casa (n + 1, 1). Queremos mostrar que é impossível a Amélia escapar. Como todas as casas da diagonal foram escolhidas, a Amélia não pode ter escolhido uma linha e uma coluna indexada pelo mesmo número, o que significa que o conjunto I dos índices das linhas escolhidas é complementar do conjunto J dos índices das colunas escolhidas (uma vez que a cardinalidade de cada um é n e são disjuntos).
• Suponhamos que 1 ∈ I (1 pertence ao conjunto I). Então, como (1, 2) foi atacada, a coluna 2 não pode ter sido escolhida, logo a linha 2 foi escolhida. Mas agora (2, 3) foi atacada, pelo que pelo mesmo raciocínio 3 ∈ I e assim por diante até n + 1 ∈ I . Isto implica que foram selecionadas n + 1 linhas, o que é impossível. Assim, 1 teria de estar em J , o que como (n + 1, 1) foi selecionada implica que n + 1 ∈ J.
• Se alguma linha com índice 1 < k < n + 1 for selecionada o argumento acima, como (k, k + 1) foi atacada, implica {k,k+1,k+1,···,n+1} ⊆ I (o conjunto está contido em I), pelo que n+1 ∈ I ∩ (intersecção com) J o que não pode acontecer. Então {1, …, n + 1} ⊆ J , o que por sua vez é também impossível. Concluímos assim que não há qualquer forma da Amélia colocar as suas peças de forma a não ter pelo menos uma delas atingida.

Três veraneantes, A, B e C, costumam fazer uma corrida matinal numa praia de Albufeira. Num certo dia, encontraram-se num ponto da praia e começaram a correr ao mesmo tempo, cada um ao seu ritmo, que mantiveram durante toda a corrida. Cada vez que chegavam a um dos extremos da praia, invertiam o sentido. Cada par de corredores nunca se encontrou nos extremos da praia. No momento em que A, B e C estavam novamente todos juntos, decidiram terminar a corrida. Para além dos momentos inicial e final, A encontrou B seis vezes e encontrou C oito vezes. Quantas vezes se encontraram B e C? B e C encontraram-se 8 vezes.

• Se o veraneante X é mais rápido do que o veraneante Y , então em cada percurso de X de um extremo ao outro da praia, X encontra Y exatamente uma vez (no percurso inicial e final esse encontro ocorreu no ponto de partida e no ponto de chegada).
• Portanto o mais rápido dos veraneantes A e B realizou 6 percursos e o mais rápido dos veraneantes A e C realizou 8 percursos.
• Assim, C é mais rápido do que A e do que B e realizou 8 percursos. Portanto B e C encontraram-se 8 vezes.

Na República do Unistão existem n estradas nacionais, cada uma ligando exatamente duas cidades, sendo sempre possível viajar entre quaisquer duas cidades percorrendo uma sequência de estradas. O Presidente do Unistão mandou numerar as estradas nacionais de 1 até n, lembrando uma lei antiga: sempre que uma cidade seja servida por mais do que uma estrada, o máximo divisor comum dos seus números tem que ser um. Mostra que é possível numerar as estradas sem violar a lei. A prova está expressa no texto seguinte.

• Para numerar as estradas procederemos da seguinte forma. Escolhemos uma cidade ao acaso e começamos a viajar escolhendo em cada cidade uma estrada ainda não visitada anteriormente. Prosseguimos até chegarmos a uma cidade servida apenas por estradas já anteriormente visitadas. Numeramos as estradas que percorremos pela ordem em que o fizemos a começar em 1. Todas as cidades visitadas cumprem agora a propriedade pretendida: a cidade inicial é servida pela estrada 1, logo o máximo divisor comum de todas as estradas que passam por ela será 1; nas cidades intermédias chegamos por uma estrada i e saímos por uma estrada i + 1 e como o máximo divisor comum de dois números consecutivos é 1, também verificam a propriedade; por fim, a cidade final ou é apenas servida por uma estrada (e nesse caso não viola a lei do Unistão) ou tem mais estradas que já foram visitadas, pelo que está numa das situações anteriores e já está em conformidade com a lei.
• Escolhemos agora, caso exista, uma cidade já visitada que ainda tenha estradas não numeradas partindo dela e repetimos o procedimento, usando apenas estradas ainda não numeradas e começando a numeração a partir do primeiro número ainda não utilizado. Repetimos o procedimento enquanto for possível.
• Pelo que vimos acima, todas as cidades visitadas estarão automaticamente em conformidade com a lei pelo que basta argumentar que todas as cidades serão eventualmente visitadas. Mas sabemos pelo enunciado do problema que para qualquer cidade há uma sequência de estradas que a liga à cidade que escolhemos como inicial, pelo que a visitaremos.

A Helena e o Luís vão jogar um jogo com dois sacos de berlindes. Eles jogam alternadamente e cada jogada consiste num dos seguintes movimentos:

• Retirar um berlinde de um dos sacos;
• Retirar um berlinde de cada um dos sacos;
• Passar um berlinde de um saco para o outro.

Ganha quem deixar ambos os sacos vazios. Antes de começar a jogar, a Helena contou os berlindes de cada um dos sacos e disse ao Luís: “Podes começar tu!”, enquanto pensava: “Assim vou ganhar de certeza!”. De que formas poderiam estar distribuídos os berlindes pelos sacos? A explicação está no texto aqui em baixo.

• Designe-se por PP uma situação em que ambos os sacos têm um número par de berlindes, por PI quando um dos sacos tem um número par de berlindes e o outro tem um número ímpar e por II quando ambos os sacos têm um número ímpar de berlindes.
• Se inicialmente se tiver uma situação PP, depois da jogada do Luís há apenas dois resultados possíveis: PI ou II. Em cada um dos casos, a Helena pode voltar a uma situação PP, diminuindo o número total de berlindes. Assim, eventualmente a Helena chegará à situação em que ambos os sacos estão vazios e portanto ganha o jogo.
• Se inicialmente se tiver uma situação PI ou II, o Luís pode retirar berlindes para obter uma situação PP e portanto eventualmente ganhará o jogo.

Um número de telefone de nove algarismos abcdefghi é memorizável se a sequência dos quatro algarismos iniciais abcd se repete na sequência dos cinco algarismos finais efghi. Quantos números memorizáveis de nove algarismos existem? Há 2 × 10⁵ − 10 números de 9 dígitos em que a sequência dos primeiros 4 dígitos se repete na sequência dos 5 dígitos finais.

• Seja abcdefghi um número com 9 dígitos. Para que a sequência dos primeiros 4 dígitos se repita na sequência dos 5 dígitos finais, então ou “abcd” = “efgh” ou “abcd” = “fghi”.
• Como há 10 algarismos possíveis para cada dígito, o número de possibilidades para a sequência inicial é 10 × 10 × 10 × 10 = 10⁴.
• Suponhamos que “abcd” = “efgh”. Então, como há também 10 possibilidades para o valor de i, há 10⁴ × 10 = 10⁵ números com 9 dígitos tais que “abcd” = “efgh”. Da mesma forma, há 10⁵ números com 9 dígitos em que “abcd” = “fghi”.
• Então para contarmos os números de 9 dígitos abcdefghi em que “abcd” = “efgh” ou “abcd” = “fghi” devemos subtrair a 10⁵ + 10⁵ o número de casos em que tanto “abcd” = “efgh” como “abcd′′ = “fghi′′. Mas “abcd”=“efgh”como“abcd”=“fghi”implica que a=e=f, b=f =g ,c=g=h e d=h=i, pelo que necessariamente todos os dígitos têm que ser iguais.
• Há, assim, 10 casos em que “abcd” = “efgh” e “abcd” = “fghi”. Em conclusão, há 2 × 10⁵ − 10 números de 9 dígitos em que a sequência dos primeiros 4 dígitos se repete na sequência dos 5 dígitos finais.

Na Capela dos Ossos estão várias velas do mesmo tamanho. No primeiro dia acende-se uma vela durante uma hora. No segundo dia, acendem-se duas velas, durante uma hora, no terceiro dia acendem-se três velas, durante uma hora, e assim sucessivamente, até ao último dia, em que se acendem todas as velas, durante uma hora. No fim desse dia, todas as velas ficam completamente gastas. Determina todas as possibilidades para o número de velas. A solução está apresentada aqui em baixo.

• Sejam n o número de velas e x o número de horas que cada uma das velas dura. O número total de horas que as velas duram é S = nx. Ora, como no primeiro dia se gasta 1 destas horas, no segundo 2 e assim sucessivamente até ao dia n, temos que S = 1+2+…+n. Logo:

• Temos então x = S ⁄ n = (n + 1) / n. Como cada vela foi acesa um número inteiro de vezes durante uma hora de cada vez, x tem de ser um número inteiro, logo n não pode ser par.
• Vejamos agora que para qualquer n ímpar, há um modo de acender as velas tal que ao fim dos n dias todas arderam o mesmo número de horas. Para k = 1, . . . , (n – 1) / 2, no dia k acendemos um qualquer conjunto de k velas e no dia n − k acendemos as n − k velas que não foram acesas no dia k. No dia n acendemos todas as velas. Assim, cada uma das velas foi acesa exactamente uma vez, ou no dia k, ou no dia n − k e no último dia foram todas acesas. Concluímos que assim todas as velas foram acesas durante o mesmo tempo.

Em cada dia, mais de metade do habitantes de Évora come sericaia à sobremesa. Mostra que há um grupo de 10 eborenses tais que, nos últimos 2010 dias, em cada dia pelo menos um deles comeu sericaia à sobremesa. A explicação está aqui em baixo.

• Sejam E o conjunto constituído pelos habitantes de Évora, na cardinalidade de E e S_i, i=1, …, 2010, os subconjuntos de E que correspondem aos eborenses que comeram sericaia há i dias. O problema consiste em demonstrar que existe um subconjunto F de E com 10 elementos que intersecta todos os subconjuntos S_i.
• Comecemos por verificar que existe um elemento de E que está em pelo menos 1006 dos subconjuntos S_i. De facto, se assim não fosse, a soma das cardinalidades dos conjuntos S_i seria menor ou igual a n × 1005. Mas, como cada S_i tem mais de n/2 elementos, esta soma é maior de (n/2) × 2010 = n × 1005, levando a uma 22 contradição. Escolhemos este elemento de E para F . Com um raciocínio análogo, mostramos que existe um segundo elemento de E que está contido em pelo menos 503 dos 1004 restantes subconjuntos e escolhemos este segundo elemento de E para F. Prosseguimos sempre com o mesmo argumento para mostrar que existem:
• Um terceiro elemento de E que está contido em pelo menos 251 dos 501 subconjuntos restantes // um quarto elemento de E que está contido em pelo menos 126 dos 250 subconjuntos restantes, // um quinto elemento de E que está contido em pelo menos 63 dos 124 subconjuntos restantes // um sexto elemento de E que está contido em pelo menos 31 dos 61 subconjuntos restantes // um sétimo elemento de E que está contido em pelo menos 16 dos 30 subconjuntos restantes // um oitavo elemento de E que está contido em pelo menos 8 dos 14 subconjuntos restantes // um nono elemento de E que está contido em pelo menos 4 dos 6 subconjuntos restantes.
• E, finalmente, que há um décimo elemento de E que está contido nos dois ú ltimos subconjuntos. O conjunto F formado por estes 10 elementos satisfaz o enunciado.

Dividiu-se uma circunferência em n partes iguais. Em cada uma destas partes foi colocado um único número de 1 a n de modo que a distância entre números consecutivos é sempre a mesma. Os números 11, 4 e 17 ficaram em posições consecutivas. Em quantas partes se dividiu a circunferência? A circunferência foi dividida em 20 partes.

• Se 11, 4, 17 ficaram em posições consecutivas também ficaram em posições consecutivas os números 10, 3, 16; os números 9,2,15; os números 8,1,14; os números 7,n,13; os números 6,n−1,12; os números 5,n−2,11; os números 4, n−3, 10; os números 3, n−4, 9; os números 2, n−5, 8, os números 1, n−6, 7, e assim sucessivamente. Na posição imediatamente a seguir ao 4 ficou o número 17 e também o n − 3, logo n = 20.
• Pela análise dos trios apresentados pode-se concluir que a circunferência foi dividida em 20 partes e os números ficaram pela seguinte ordem: 1, 14, 7, 20, 13, 6, 19, 12, 5, 18, 11, 4, 17, 10, 3, 16, 9, 2, 15, 8.

O Duarte quer desenhar um quadrado com 2009 cm de lado, dividido em 2009 × 2009 quadrículas de lado 1 cm, sem levantar o lápis. Partindo de um canto do quadrado, qual é o comprimento da linha mais curta que permite fazer este desenho? O Duarte tem de percorrer 8080196 cm com o lápis.

• Designe-se cada lado de uma quadrícula por aresta.
• O comprimento total das arestas a desenhar é 2×2009× 2010 cm. Consideremos os 4 × 2008 = 8032 cruzamentos de onde saem três arestas, designados por um T. O Duarte tem que passar o lápis duas vezes em cada T , logo no seu caminho terá que repetir uma aresta que sai de cada T. Como cada uma das arestas repetidas só pode incidir em dois T, então o Duarte tem que repetir pelo menos 8032/2 = 4016 arestas.
• Ora o percurso indicado na figura seguinte repete exatamente 4016 arestas, logo este é o número mínimo de repetições que o Duarte tem que efetuar.
• Assim, o Duarte tem que percorrer 2 × 2009 × 2010 + 4016 = 8080196 cm com o lápis.

O Nelson desafia a Telma para o seguinte jogo: primeiro a Telma retira 29 números do conjunto {0, 1, 2, 3, …, 1024}, em seguida o Nelson retira 28 números dos restantes. Depois a Telma retira 27 números e assim sucessivamente, até restarem apenas 2 números. O Nelson terá de dar à Telma a diferença entre estes dois números em euros. Qual é a maior quantia que a Telma pode ganhar independentemente da estratégia do Nelson? A quantia é 32.

• A Telma consegue garantir pelo menos 32 euros. Para isso, apenas necessita de, em cada jogada, retirar os números que estão numa posição par quando estes estão por ordem crescente. De facto, com esta estratégia, a distância mínima entre dois números do conjunto é pelo menos duplicada em cada jogada, pelo que ao fim das cinco jogadas da Telma, esta distância é no mínimo 2⁵ = 32.
• O Nelson consegue evitar pagar mais de 32 euros. Para isso, apenas necessita de, em cada jogada, retirar todos os números do início, ou todos os números do final, ficando com aqueles cuja distância máxima é menor. De facto, com esta estratégia, a distância máxima entre dois números do conjunto é pelo menos dividida por dois em cada jogada, pelo que ao fim das cinco jogadas do Nelson, esta distância é no máximo 1024/(25) = 32.

O João tinha pérolas azuis, brancas e vermelhas e com elas construiu um colar com 20 pérolas que tem tantas pérolas azuis como brancas. O João reparou que, independentemente do modo como cortasse o colar em duas partes, ambas com um número par de pérolas, uma das partes teria sempre mais pérolas azuis do que brancas. Quantas pérolas vermelhas tem o colar do João? Tem duas.

• O colar não tem duas pérolas vermelhas lado a lado. Se o colar tivesse duas pérolas vermelhas lado a lado, então seria possível separar essas duas pérolas das outras. O colar ficaria assim separado em duas partes, tendo cada uma dessas partes o mesmo número de pérolas azuis e de pérolas brancas.
• O colar não tem uma pérola azul e uma pérola branca lado a lado. Se tivesse, então bastaria separar essas duas pérolas das outras para separar o colar em duas partes, tendo cada uma delas o mesmo número de pérolas azuis e de pérolas brancas.
• O número de pérolas vermelhas não pode ser zero porque nesse caso existiria uma pérola azul ao lado de uma pérola branca.
• Uma vez que o número de pérolas vermelhas é par, o colar tem pelo menos duas pérolas vermelhas. Além disso, entre duas pérolas vermelhas consecutivas só há pérolas da mesma cor.
• Pelo menos uma das pérolas vermelhas tem uma sucessão de pérolas azuis de um lado e uma sucessão de pérolas brancas no outro. Suponha-se que o comprimento da sucessão de pérolas azuis é menor ou igual do que o da sucessão de pérolas brancas. Deste modo, existe no colar uma sucessão de pérolas do tipo:

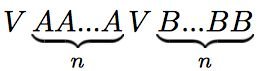
• Essa sucessão tem tantas pérolas azuis como brancas.Logo, o resto do colar também tem um número igual de pérolas azuis e brancas e, por isso, esta sucessão tem de ser a totalidade do colar. Assim, o colar tem duas pérolas vermelhas, nove azuis e nove brancas.

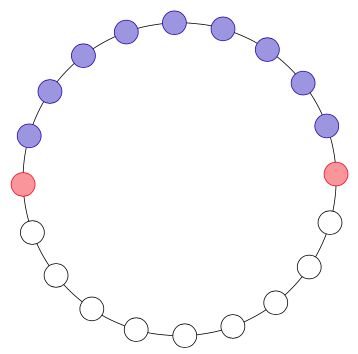
• Resta verificar que este colar está nas condições do enunciado. Corte-se o colar em duas partes com um número par de pérolas cada uma. Se uma das partes não tiver pérolas vermelhas, então só tem pérolas azuis ou só tem pérolas brancas, portanto uma das partes tem mais pérolas azuis do que brancas. Se em cada uma das partes há uma pérola vermelha, então uma das partes tem mais pérolas azuis e a outra mais pérolas brancas.

A rua do António tem 100 casas numeradas de 1 a 100. Qualquer casa numerada com a diferença dos números de duas casas da mesma cor é de uma cor diferente. Mostra que na rua do António há casas de, pelo menos, cinco cores diferentes. A explicação segue no próximo texto.

• Suponha-se que as 100 casas são, quando muito, de quatro cores diferentes. Neste caso, há pelo menos 25 casas da mesma cor. Considere-se que essa cor é o amarelo. Sejam x₁, x₂,…,x₂₅ os números dessas 25 casas ordenados de forma crescente. Os números x₂₅ − x₂₄ , x₂₅ − x₂₃, …, x₂₅− x₁ são todos diferentes e as casas com esses números são das outras três cores. Pelo menos oito dessas casas são da mesma cor, que se supõe ser a cor branca.
• Sejam a₁, a₂, …, a₈ os números dessas oito casas ordenados de forma crescente. Para cada i = 1,…,8, a_i =x₂₅−x_ki com ki um número inteiro entre 1 e 24, logo a_i−a_j =(x₂₅−x_ki)−(x₂₅−x_kj)=x_kj −x_ki, ou seja, a diferença entre dois dos números a₁,a₂,…,a₈ é ainda a diferença entre dois dos números x₁,x₂,…,x₂₅. Tem-se assim que os números a₈ − a₇,…, a₈ − a₁ são todos diferentes e as respectivas casas não são nem brancas, nem amarelas. Portanto, pelo menos quatro dessas casas são da mesma cor que se supõe ser a cor azul.
• Sejam b₁, b₂, b₃, b₄ os números dessas quatro casas azuis ordenados de forma crescente. Tal como se viu anteriormente, a diferença entre dois desses números é igual à diferença entre dois dos números a₁, a₂, …, a₈, que por sua vez é igual à diferença entre dois dos números x₁ , x₂ , …, x₂₅ .
• Como se supôs que as casas são, no máximo, de quatro cores diferentes, as casas com os números b₄ − b₃, b₄ − b₂, b₄ − b₁, b₃ − b₂, b₃ − b₁, b₂ − b₁ são de uma quarta cor, por exemplo, cor-de-rosa. Mas (b₄ − b₂) − (b₄ − b₃) = b₃ − b₂ e, por isso, existem duas casas cor-de-rosa tais que a casa cujo número é igual à diferenc ̧a dos seus números é também cor-de-rosa, o que é impossível. Chega-se assim à conclusão que as casas são de, pelo menos, cinco cores.

O Alexandre e o Herculano estão na estação de Campanhã à espera do comboio. Para se entreterem, decidem calcular o comprimento de um comboio de mercadorias que passa pela estação sem alterar a velocidade. Quando a frente do comboio passa por eles, o Alexandre começa a andar no sentido do movimento do comboio e o Herculano começa a andar no sentido oposto. Os dois caminham à mesma velocidade e cada um deles pára no momento em que se cruza com o fim do comboio. O Alexandre andou 45 metros e o Herculano 30. Qual é o comprimento do comboio? É de 180 m de comprimento.

• O Alexandre andou mais 45−30 = 15 metros do que o Herculano e, no período de tempo que o Alexandre demorou a percorrer esses 15 metros, o comboio andou 45 + 30 = 75 metros. Portanto, no mesmo período de tempo, o comboio percorre 75/15 = 5 vezes mais metros do que cada um dos rapazes.
• Assim, enquanto o Herculano andou 30 metros, o comboio andou 30 × 5 = 150 metros. Como o Herculano começou a andar quando foi passado pela frente do comboio, parou quando se cruzou com o fim do comboio e andou 30 metros no sentido oposto,então o comboio tem 150+30=180 metros de comprimento.

Numa fila para um concerto do Super Rock Pop estavam 2005 pessoas.Com o objectivo de oferecer 3 entradas para o “backstage”, pediu-se à primeira pessoa da fila que gritasse “Super”, à segunda “Rock”, à terceira “Pop”, à quarta “Super”, à quinta “Rock”, à sexta “Pop” e assim sucessivamente. Quem disse “Rock” ou “Pop” foi eliminado. Repetiu-se este processo, sempre a partir da primeira pessoa da nova fila, até restarem apenas 3 pessoas. Em que posição se encontravam no início essas pessoas? Nas posições 1, 730 e 1459.

• Numerem-se as pessoas da fila de 1 a 2005.
• Após cada uma das pessoas ter gritado uma vez, não foram eliminados os números que têm resto 1 quando divididos po 3. Assim, restaram os 669 números da forma 3_k1+1, k1=0, 1,…,668, ou seja, 1, 4, 7, 10, 13, 16, …, 2002, 2005. Observe-se que estes números podem ser representados pelo índice k1, que começa em zero. Logo, destes 669 números não foram eliminados os 223 números da forma 3_k1+1,com k1 = 3_k2 e k2 = 0,…, 222.
• Uma vez que 222 = 3×74, 74 = 3×24+2, 24 = 3×8 e 8 = 3×2+2, conclui-se que, após cinco repetições do processo, não foram eliminados os três números da forma 3_k1 + 1, com k1 =3_k2, k2 =3_k3, k3 =3_k4, k4 =3_k5, k5 =3_k6 e k6 =0, 1 e 2.
• Assim, as pessoas que ganharam as entradas estavam inicialmente nas posições 3⁶_k6+1, para k6= 0, 1 e 2, ou seja, 1, 730 e 1459.