Nas últimas semanas, muito se tem falado sobre curvas, epidemias, pandemias e afins. Além da Saúde Pública, Epidemiologia e Virologia, por razões óbvias, os dados, os números, os modelos, no fundo a Matemática e a Estatística, entraram em força na comunicação social. No entanto, quantidade nem sempre significa qualidade. Impressiona a quantidade de pessoas não versadas em matemática, estatística ou epidemiologia que têm tecido considerações com algum impacto nos media e na sociedade sobre a propagação da Covid-19. Na realidade, é uma atividade bastante arriscada porque todos podemos fazer contas, mas nem todos compreendem os pressupostos envolvidos, fundamentais para perceber se uma análise é de facto útil e informativa ou apenas escusada e enganadora.
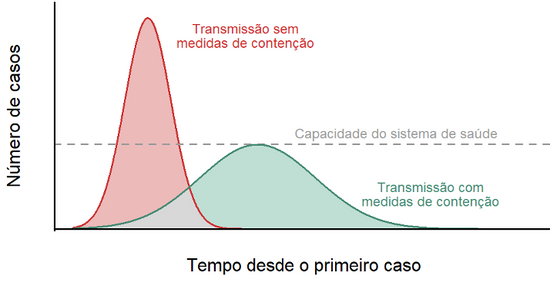
A imagem didática da tão falada curva epidémica, repetida vezes sem fim, pode ter leituras muito inapropriadas. Esta curva representa a evolução ao longo do tempo do número de novos casos. E só no fim da epidemia, com os dados existentes, é que a podemos reconstruir a evolução da pandemia na sua totalidade. Antes, só podemos fazer previsões e construção de cenários, baseados em modelos. Os modelos são aproximações da realidade. Ou seja, não devem ser confundidos com a realidade, mas podem ser muito úteis. É com base em modelos que se tenta prever quando será o “pico”, isto é, quando é de esperar que a curva comece na sua fase descendente.
dr
Se a forma será mais próxima da curva a vermelho ou da curva a verde, não podemos dizer desde logo, mas podemos começar a ter uma perceção de qual delas será à medida que o tempo passa. Contudo, só no fim saberemos e mesmo assim teremos uma aproximação da realidade, não a realidade!
Um leitor inadvertido, mas com alguns conhecimentos básicos de probabilidade e estatística, poderá associar esta imagem à famosa curva de Gauss ou distribuição Normal. No entanto, as aparências iludem, pois, o número de novos casos tem a particularidade de estar indexado ao dia, isto é, há uma evolução ao longo do tempo. Esta indexação temporal (no eixo horizontal) faz com que o número de novos casos (números inteiros, no eixo vertical) não possa ser tratado como se fosse um simples conjunto de dados recolhidos aleatoriamente na população. E isso é intuitivo. Naturalmente, o número de novos casos num dia depende do número de casos existentes até esse dia.
Em termos técnicos, quando se tem dados de uma medição sem esta indexação temporal, é habitual fazer um gráfico (designado por histograma), para tentar explorar possíveis modelos teóricos de distribuição de probabilidade relativa aos dados. Para tal representa-se no eixo horizontal essa medição, em intervalos, e no eixo vertical a sua frequência, adaptando então uma “curva” a essa figura (a qual pode até ser, eventualmente, a dita curva de Gauss). Paralelamente, também é costume calcular diversas medidas (e.g., média, mediana, desvio-padrão) e, às vezes, as medidas de achatamento ou curtose. Ora, para o número de novos casos representativos da evolução de uma epidemia, aquela representação gráfica e aquelas medidas não servem de nada, pois estão a ignorar a indexação temporal que contém a essência da estrutura do fenómeno epidémico em estudo. Por estas, e outras razões, também as medidas de achatamento, tipicamente comparadas à correspondente da distribuição Normal, usadas para estudar o achatamento de uma “curva” representativa de uma distribuição de probabilidade, não fazem qualquer sentido para dados relativos à evolução de uma epidemia. A curva epidémica não tem nada a ver com esta última “curva” — a da distribuição de probabilidade. A curva epidémica até poderá estar a achatar, mas a evidência não deriva de modo algum destas medidas de achatamento, tal como se pretendia num texto recentemente publicado no Observador a 1 de abril. Nada se pode inferir desta medida para concluir do achatamento da curva epidémica. Não há qualquer relação entre uma coisa e outra. Medem realidades totalmente diversas.
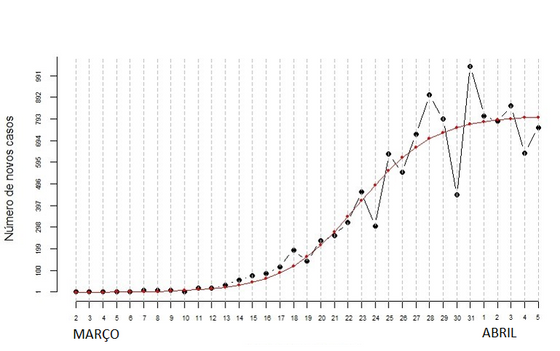
Ao tentar analisar os primeiros dias de uma epidemia temos apenas uma parte da curva epidémica, não o todo. Numa fase inicial, até poderá ser a curva exponencial aquela que melhor descreve os dados, como tanto já se discutiu, ou seja, o melhor modelo ou a melhor aproximação da realidade, a partir da qual podemos fazer previsões úteis. Mas essas previsões têm um prazo de validade curto. Ao avançar um pouco mais no tempo, o modelo exponencial deixa de representar a evolução epidémica porque a curva começa a achatar. Isto é natural já que, para além de outros constrangimentos, não há uma quantidade infinita de pessoas para serem infetadas. Os dados serão melhor descritos de outra forma, por exemplo, considerando uma curva logística, ou outra. Veja-se na figura a situação de Portugal no dia 5 de abril, onde se tentou adaptar um modelo (curva) ao número de novos casos confirmados pelas autoridades até à data.
A 5 de abril, segundo os dados reportados pela DGS, tinha-se a seguinte evolução temporal do número de novos casos em Portugal, onde se ajustou uma curva (a vermelho), baseada num modelo, parte de uma possível curva epidémica teórica:
dr
Claro que a sociedade civil, a comunicação social e os decisores políticos gostariam de ter previsões sobre o “famoso pico” e sobre o fim desta dura pandemia. Note-se que o pico — a existir um, porque um modelo não é a realidade — não é o fim, é apenas o início da fase descendente. Ao atingir o pico os cuidados têm de se manter para não se voltar atrás.
No entanto, sem o tempo e sem os dados suficientes, a incerteza é muita. Não será essa a razão pela qual aqueles que verdadeiramente compreendem a noção de variabilidade e a dificuldade que existe na utilização de modelos para prever o futuro não o fazem? Serão estes modelos úteis? Certamente são, embora não tanto pelos resultados de cada modelo individual, mas porque nos permitem criar cenários, ajudar a planear e avaliar estratégias. Nos últimos tempos, o rigor do conhecimento científico tem sido muitas vezes sacrificado pela comunicação social em nome do direito à informação. É dever dos investigadores, especialistas nas suas áreas de conhecimento, desmistificar informação e divulgá-la à comunicação social para que esta a possa transmitir de forma fidedigna. Foi esta a razão que nos levou a escrever este texto.
As várias áreas (virologia, estatística, epidemiologia, saúde pública, religião, política, ética…) representam as diferentes peças de um puzzle, mas cada peça tem uma fronteira única. Um especialista sobre vírus deve abster-se de tecer comentários sobre modelos e predições, assim como um especialista sobre modelos deve abster-se de tecer comentários sobre o vírus. O que precisamos agora é de equipas de cientistas com valências complementares a trabalhar em conjunto para resolver um problema comum e depois, alguém para comunicar os resultados. Na verdade, salvo raras exceções, essa comunicação também deveria ser feita por um profissional de comunicação de ciência, e não pelos cientistas. Um profissional que percebe o que os cientistas dizem e que sabe como passar para o público as informações que são fundamentais.
O direito à informação deve ser garantido, mas parece evidente que a comunicação social deve fazer um esforço extra ao escolher as suas fontes e procurar quem possa apresentar e discutir os números de forma rigorosa.












