Foram muitos, em todo o mundo, que puseram a mente a trabalhar com o exercício que os melhores alunos de Singapura resolveram durante as Olimpíadas da Matemática asiáticas. Como se desenvolve o nosso raciocínio lógico que nos leva a encontrar respostas para os quebra-cabeças?
O segredo está no cérebro: é o seu hemisfério esquerdo, o mais exercitado em 98% dos humanos, o responsável pelo pensamento lógico e pela capacidade de comunicação.
Quando exposto a situações difíceis em que a ação se torna mais urgente, a sua atividade aumenta para nos ajudar a encontrar o caminho mais curto para a solução. Trabalha para encontrar uma estratégia e sequenciar as ações: desenvolvemos o pensamento abstrato, a fluidez do pensamento, a determinação e a atenção.
Mas como funciona o raciocínio? Há uma disciplina que estuda a sua estrutura, a lógica. No raciocínio lógico a regra determina-se pela indução, a premissa pela abdução e a conclusão é formulada através da dedução.
Ciência a mais? Não desespere. Perceba mesmo o que acontece porque estas capacidades são muito usadas em testes psicotécnicos. E essas avaliações são úteis, por exemplo, para determinar se alguém é adequado a um emprego que exija uma determinada característica psicológica.
Mas o que importa mesmo é ginasticar o cérebro. Por isso, o Observador apresenta-lhe cinco quebra-cabeças que vão pôr a sua mente a trabalhar. Alguns são usados em entrevistas de emprego. Outros nas faculdades. Atreva-se a resolvê-los. No final do artigo, encontra as soluções para os problemas.
1 — QUEM TEM UM PEIXE COMO ANIMAL DE ESTIMAÇÃO?
Este quebra-cabeças só terá sido resolvido com sucesso por 2% das pessoas. É um dos exercícios de raciocínio lógico mais desafiantes e complexo. Criado por Einstein.
- Há cinco casas, todas com cores diferentes.
- Em cada casa mora uma pessoa, todas com nacionalidades diferentes.
- Os gostos dos cinco vizinhos são completamente diferentes uns dos outros.
- Nenhum deles vive com o mesmo animal de estimação, não fumam a mesma marca de cigarros, nem bebem a mesma marca de bebida.
Para tal, tome atenção aos seguintes dados:
- O inglês vive na casa vermelha.
- O sueco tem cachorros.
- O dinamarquês bebe chá.
- A casa verde fica do lado esquerdo da casa branca.
- O homem que vive na casa verde bebe café.
- O homem que fuma Pall Mall cria pássaros.
- O homem que vive na casa amarela fuma Dunhill.
- Quem vive na casa do meio bebe leite.
- O norueguês vive na primeira casa.
- Quem fuma Blends vive ao lado de quem tem gatos.
- O que cria cavalos vive ao lado do homem que fuma Dunhill.
- O homem que fuma BlueMaster bebe cerveja.
- O alemão fuma Prince.
- O norueguês vive ao lado da casa azul.
- Quem fuma Blends é vizinho do homem que bebe água.
2 — QUAL É A PERGUNTA QUE FARÁ A DIFERENÇA ENTRA A VIDA E A MORTE?
Imagine que está numa sala que tem duas portas, cada uma delas com um guardião.
Um deles diz sempre a verdade e outro diz sempre a mentira.
Para escapar da sala onde está precisa de escolher uma das portas: há uma que o leva para a vida, outra que o leva para a morte.
Embora não consiga descobrir a diferença entre as duas portas nem entre os dois guardiões, há uma pergunta que pode fazer para descobrir qual a porta certa. Qual é?
3 — QUEM PODE SALVAR OS QUATRO HOMENS E ESCAPAR AO PSICOPATA?
Quatro homens – Armando, Bernardo, Carlos e Daniel – foram raptados por um psicopata.
Quando acordaram, estavam enterrados em areia, apenas com a cabeça de fora.
Em cada um deles foi posto um chapéu, azul ou vermelho.
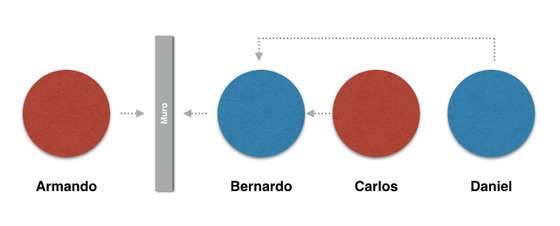
Armando tem um chapéu vermelho, está virado para a direita e só consegue ver um muro.
Do outro lado do muro estão Bernardo com um chapéu azul, Carlos com um chapéu vermelho e Daniel com outro chapéu azul. Estão todos em fila virados para a parede. Deste modo:
- Daniel consegue ver Bernardo e Carlos à sua frente e sabe que Armado está do outro lado da parede.
- Carlos consegue ver Bernardo à sua frente. Sabe que Armando está do outro lado da parede e que Daniel está imediatamente atrás de Carlos.
- Bernardo apenas consegue ver a parede, mas sabe que Carlos está atrás dele e que Daniel está atrás de Carlos.
- Armando só consegue ver a parede e sabe que Bernardo, Carlos e Daniel estão do outro lado dela.
O psicopata diz-lhes:
Há dois chapéus vermelhos e dois chapéus azuis. Se algum de vós disser corretamente a cor do próprio chapéu, todos serão libertados. Se nenhum de vós acertar, todos vão ser mortos.
Os quatro homens não podem conversar entre eles, mas não podem virar a cabeça nem sequer olhar para cima.
Quem pode salvar os quatro homens?
4– QUAL É O DEUS VERDADEIRO, O FALSO E O ALEATÓRIO?
Os deuses de Boolos: este teste foi desenvolvido pelo filósofo americano George Boloos e publicado na The Harvard Review of Philosophy. Na altura, o artigo recebeu o título “O quebra-cabeças mais difícil de sempre”.
Existem três deuses: o Verdadeiro, o Falso e o Aleatório.
O deus Verdadeiro diz sempre a verdade, o deus Falso diz sempre mentiras e o deus Aleatório pode dizer a verdade ou a mentira, aleatoriamente.
Tem de descobrir qual dos três é o deus Verdadeiro, Falso ou Aleatório.
Para tal, tem de fazer perguntas de “sim ou não” a um deus de cada vez. O problema é que os deuses não respondem em português, mas antes na língua deles. Verdadeiro, Falso e Aleatório vão responder “da” ou “ja”, mas nós não sabemos qual destas palavras é a resposta positiva ou a negativa.
O exercício exige que saiba o seguinte:
- Pode perguntar mais que uma pergunta a um dos deuses mas, por consequência, nenhuma a outro deus.
- O teor da segunda pergunta e a quem ela se dirige pode estar dependente da resposta à primeira, e assim sucessivamente.
- As respostas de Aleatório são uma questão de acaso, com as mesmas probabilidades de lançar uma moeda ao ar e calhar “cara” ou “coroa”.
- Aleatório vai responder “da” ou “ja” perante qualquer pergunta de “sim ou não”.
5 — COMO SE RESOLVEM ESTAS CONTAS BARALHADAS?
| 8809 = 6 | 5555 = 0 |
| 7111 = 0 | 8193 = 3 |
| 2172 = 0 | 8096 = 5 |
| 6666 = 4 | 1012 = 1 |
| 1111 = 0 | 7777 = 0 |
| 3213 = 0 | 9999 = 4 |
| 7662 = 2 | 7756 = 1 |
| 9313 = 1 | 6855 = 3 |
| 0000 = 4 | 9881 = 5 |
| 2222 = 0 | 5531 = 0 |
| 3333 = 0 | 2581 = ??? |
Descubra que valor iguala ao número “2581”, tendo em conta todas as equivalências dadas anteriormente.
As soluções
1
Talvez seja mais simples se construir uma tabela onde as colunas representam as casas e em que cada uma das linhas se possa inserir as características.
| Primeira Casa | Segunda Casa | Terceira Casa | Quarta Casa | Quinta Casa | |
| Cor | Amarelo | Azul | Vermelho | Verde | Branca |
| Nacionalidade | Norueguês | Dinamarquês | Inglês | Alemão | Sueco |
| Bebida | Água | Chá | Leite | Café | Cerveja |
| Cigarro | Dunhill | Blends | Pall Mall | Prince | BlueMaster |
| Animal | Gatos | Cavalo | Pássaros | Peixes | Cachorros |
O segredo está em começar sempre pelas dicas mais simples: comece por utilizar as dicas que se referem à ordem das casas, por exemplo, “o norueguês mora na primeira casa”. A partir daí, aumente o nível de dificuldade das dicas que utilizar.
Assim, torna-se mais fácil deduzir as características umas pelas outras.
2
A pergunta que deve expor a um dos guardiões é: “Se eu perguntasse ao outro guardião que porta me leva de volta à vida, o que me diria ele?”. A porta que o guardião indicar vai sempre conduzir à morte, por isso há que escolher a Contrária.
Porquê?
Se perguntar ao guardião que diz a verdade, ele vai assumir que o outro guardião vai mentir e mostrar a porta para a morte.
Da mesma forma, se perguntar ao guardião que diz a mentira, ele vai indicar a porta para a morte porque o guardião honesto iria mostrar a porta para a vida.
3
Daniel consegue ver Carlos e Bernardo. Se ele observasse dois chapéus azuis, saberia que a cor do chapéu que tem na cabeça seria vermelho. Da mesma forma, se os dois chapéus dos amigos fossem vermelhos, o dele seria azul. Como Carlos e Bernardo têm chapéus de cor diferente, Daniel não pode saber de que cor é o seu chapéu, porque não pode verificar qual é o chapéu de Armando, que está do outro lado do muro. Portanto, nem Armando nem Daniel podem resolver o mistério.
Apercebendo-se que Daniel não diz nada, então Carlos dá-se conta que o chapéu que carrega só pode ser diferente do chapéu de Bernardo. Ora, se Carlos consegue olhar para Bernardo e reparar que o chapéu do amigo é azul, então o dele só pode ser vermelho.
4
Se assumirmos “P” como uma qualquer pergunta de “sim ou não” (És o deus Verdadeiro ou És o deus Falso?) podemos tomar em conta a seguinte questão “Q”:
Se eu lhe perguntasse “P”, responderia “ja”?
Quando um dos deuses é questionado com “Q”, a resposta “ja” vai indicar a resposta correta de “P” e a resposta “da” vai indicar a resposta errada de “P”. Isto porque, matematicamente, a união de duas respostas positivas dá outra resposta positiva e a união de uma resposta negativas também resulta numa resposta positiva.
5
É tão simples quanto o seguinte: o algarismo que iguala a cada um dos números corresponde ao número de furos dos números. Por isso 2581 é igual a 2. Só o 8 tem dois furos. O 0 tem 1. O 9 também tem um. E assim se resolve um mistério muito simples.