O número Pi é parte de nós. Está nos búzios com que fingimos ouvir o mar no verão, nas flores que oferecemos às pessoas de quem gostamos, nos eclipses que nos põem de olhos no céu, nos ponteiros dos relógios e nas proporções do corpo humano. Albert Einstein descobriu que o Pi está também nos rios que atravessam as nossas cidades. E pode ser encontrado até naquilo que faz de nós o que realmente somos: nas duplas hélices do ADN e nas pupilas dos olhos.
Por definição, Pi é a razão entre a circunferência de um círculo pelo seu diâmetro. Divida o valor de uma circunferência pelo diâmetro dela e chegará sempre ao mesmo número irracional: 3,14159265358979323… e por aí adiante, pelo infinito e mais além. Aquele que é o melhor amigo dos matemáticos pode ser um verdadeiro martírio para quem não gosta de calcular áreas de coisas redondas. Mas quando há tartes e computadores envolvidos, o Pi pode tornar-se uma boa companhia para o mais comum dos mortais.
Para celebrar o Dia do Pi, o Observador convida-o a resolver três exercícios onde esse número irracional tem mesmo de ser usado. Dois deles foram publicados no site “Brilliant.org”. Já aqui em baixo pode encontrar os enunciados dos três problemas (o primeiro serve apenas de aquecimento para a mente). Resolva-os um pouco mais em baixo no artigo.
Qual é a área de uma moeda de dois euros, sabendo que o seu diâmetro é de 25,75 mm?
Aqui em baixo estão três caixas quadradas iguais com tartes. Qual das caixas contém maior quantidade de tarte? 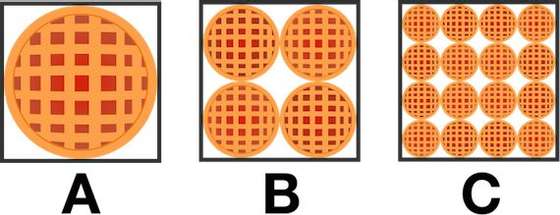
Cem computadores estão ligados através de uma grelha. A grelha tem dez colunas cada uma com dez computadores. Ao início, nove destes computadores estão infetados com um vírus. E o vírus espalha-se da seguinte maneira: se algum computador estiver diretamente ligado a pelo menos outros dois computadores infetados, ele também ganhará o vírus. O vírus vai infetar todos os computadores desta rede? 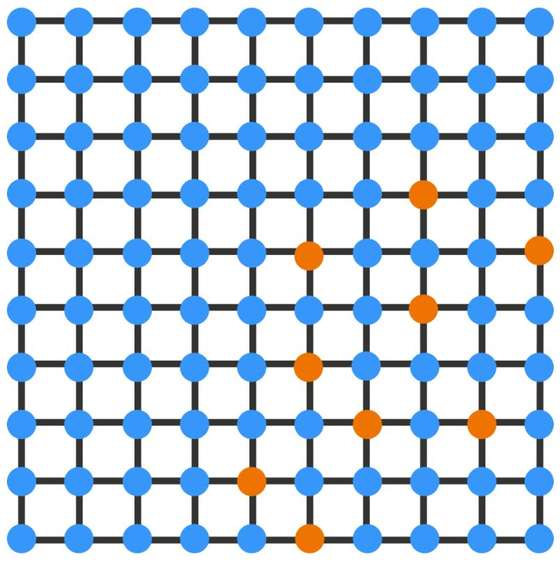
Está pronto? Pense durante uns minutos. Encontramo-nos já com as respostas prontas mais cá em baixo.
…
…
…
…
…
…
…
…
…
…
Qual é a área de uma moeda de dois euros, sabendo que o seu diâmetro é de 25,75 mm?
Para resolver este exercício é preciso ter estado atento às aulas de matemática do ensino básico. A área de um círculo consegue-se através de uma fórmula onde se multiplica o número “Pi” pela potência do raio do círculo (A = π·r2). Ora, Pi tem um valor fixo, mas para calcular o raio precisamos de saber o diâmetro. Como o raio corresponde a metade do diâmetro, então significa que r = 12,875 mm. Agora é só substituir os valores na fórmula: A = π ×12,875 × 12,875. Então, a área de uma moeda de dois euros é, aproximadamente, 520,8 milímetros quadrados.
Aqui em baixo estão três caixas iguais com tartes. Qual das caixas contém maior quantidade de tarte?
Uma das primeiras conclusões a que podemos chegar é que, se as caixas são quadradas, então todos os seus lados são iguais. Através do primeiro quadrado (A) concluímos também que o diâmetro da tarte é precisamente igual ao comprimento de um dos lados da caixa. Olhando para a caixa B, podemos concluir que cada uma das tartes tem metade do diâmetro daquela que está na primeira caixa e que as tartes da caixa C têm metade do diâmetro das tartes da caixa B. Certo é que, juntando as tartes tanto no caso da caixa B como da caixa C elas perfazem todas o mesmo diâmetro e isso significa que todas as caixas têm a mesma quantidade de tarte. Claro que também podemos recorrer à matemática. Imagine que o diâmetro da primeira tarte é de 20 centímetros e use essa informação para descobrir as áreas das tartes do exercício da mesma forma como descobrimos a área da moeda. Vai perceber que, somando as áreas das tartes da caixa B ou somando as áreas das tartes da caixa C, o valor será o mesmo da área da tarte da caixa A.
Cem computadores estão ligados através de uma grelha. A grelha tem dez colunas cada uma com dez computadores. Ao início, nove destes computadores estão infetados com um vírus. E o vírus espalha-se da seguinte maneira: se algum computador estiver diretamente ligado a pelo menos outros dois computadores infetados, ele também ganhará o vírus. O vírus vai infetar todos os computadores desta rede?
O segredo para resolver este exercício está no perímetros da infeção, ou seja, a extensão do limite da infeção. Para que a infeção chegue a todos os computadores, então o limite final deve ser 40, porque esse é o perímetro deste quadrado. O perímetro de um computador infetado é 4 porque esse é o número de computadores livres de vírus a que está ligado. Como neste exercício só há nove computadores infetados, então o número máximo de computadores com vírus será 36, que resulta da multiplicação de 9 pelo número de computadores a que cada um está ligado.













