“Por uma centésima se entra na faculdade e por uma centésima se fica fora”, o que para muitos significa não entrar no curso que pretendiam, para outros o adiamento da entrada e para alguns a exclusão do ensino superior.

O problema piora com ultrapassagens injustas. Por exemplo, um aluno com classificação de 15 em exame e 19 de classificação interna (a atribuída pela escola), mostra saber menos, mas tem uma melhor média de candidatura que outro com 16 valores em exame e na média interna.

Para tentar perceber a dimensão deste problema analisámos o período de 1998 a 2019 quanto à diferença entre classificação interna e classificação de exame. A esta diferença chamamos diferencial.

Nesta análise, com vista a dar pistas para um sistema de acesso menos injusto, é importante distinguir entre as classificações de exame positivas e negativas já que o maior diferencial ocorre nos alunos que reprovam em exame e esses não são relevantes para a análise do acesso ao ensino superior.

Para melhor analisarmos o impacto considerámos dois grandes grupos: o diferencial superior a 3 valores e o diferencial inferior a 1 valor.

Destacamos algumas leituras dos dados abaixo:

• Verifica-se um diferencial superior a 3 valores em um quarto dos exames, o que implica um benefício superior a 1 valor na nota de candidatura ao ensino superior. Foram perto de 40 mil exames em 2019.
• Existe uma grande variabilidade do nível de dificuldade dos exames finais do secundário, o que torna muito difícil às escolas controlar o diferencial.
• O diferencial decresce à medida que as classificações de exame aumentam, sendo muito grande nos alunos que reprovam em exame.
• O valor do diferencial é sensível à disciplina, à escola, à região e ao sexo.
• Talvez seja surpreendente, mas há imensos diferenciais negativos (os professores deram ao aluno pior nota do que ele conseguiu em exame). Inclusivamente, há escolas em que a média interna da escola é inferior à média que os seus alunos conseguem no exame. Em 2019 houve duas escolas nessas condições, as duas privadas.
• As injustiças no acesso ao superior são muito significativas: até 30% dos alunos (dependendo dos cursos) não entram no curso que desejam ao serem ultrapassados por colegas que em exame mostraram saber menos.

Antes de propor sistemas alternativos de acesso ao superior convém definir, em abstrato, propriedades de um sistema de acesso mais justo.

Propriedade 1. As notas de candidatura têm de estar na mesma escala.

Não faz sentido cronometrar A em minutos e B em segundos e dar a vitória a A alegando que correu 100m em 1 minuto enquanto B correu 200m em 30 segundos, e 1 é menor que 30.

Usa-se a mesma escala para avaliar conhecimentos quando todas as pessoas foram igualmente informadas do que deviam saber e quando se aplica o mesmo instrumento de avaliação a todos; para a justiça do sistema tais condições são necessárias, mas não suficientes pois se o exame em certo ano for anormalmente fácil (em 2020 a classificação mais frequente no exame nacional de matemática do 12.º ano foi 19 valores enquanto em 2021 foi 10) esses alunos estarão em vantagem ao concorrer com alunos que fizeram um exame mais difícil.

Para que os alunos estejam todos a “correr” na mesma prova e as classificações possam estar na mesma escala é preciso que cada disciplina tenha:

1. Um programa que define genericamente o que se deve aprender, por que ordem e quando.

2. Uma densificação dos programas, as chamadas “metas”, um conceito introduzido em Portugal por Isabel Alçada e depois aprofundado por Nuno Crato.

3. Uma caracterização do nível a atingir, através de um caderno de exercícios resolvidos produzido pela tutela.

4. As notas de exame precisam ser trabalhadas estatisticamente para comparabilidade de classificação em anos diferentes.

Neste momento, em Portugal, os “programas” são nebulosos, na realidade não há programas, sendo muito difícil estabilizar a dificuldade dos exames ou até saber o que se pode perguntar. Desde que no verão de 2021 o Governo terraplanou programas, metas e cadernos de exercícios das disciplinas que os tinham, na prática ficou cada escola a correr a sua corrida.

Propriedade 2. Se A sabe mais que B, é A quem deve ter preferência na escolha do curso.

Há muitos alunos a mostrar saber menos no instrumento de avaliação comum (exame nacional), mas com preferência no acesso ao superior graças à generosidade da sua classificação interna e à exigência da classificação interna de outros. Isso depois fica patente na faculdade onde, em cursos com média de entrada alta, se constata haver alunos com níveis de conhecimento muito diferentes.

É habitual dizer que colocar a decisão total no exame não é justo pois há alunos cuja ansiedade provoca a falha. Convém esclarecer que todas as pessoas em prova experimentam diversos graus de ansiedade, mas dentro de certos limites ela é benéfica. Uma ansiedade tóxica ao ponto de provocar a falha, requer ajuda profissional e quanto mais cedo melhor. Quem quer ser operado por um cirurgião cuja ansiedade para não falhar, leva a falhar? Também precisa de ajuda profissional o atleta, músico, jornalista de TV ou rádio, etc., que revele níveis de ansiedade tóxica.

Note-se que dois meses depois de acabar o secundário e entrar na faculdade, o aluno estará a fazer testes todas as semanas, avaliações em laboratório, trabalhos, etc., situações tipicamente de tudo ou nada, onde ou passa ou volta no ano seguinte. E um pouco depois estará em entrevistas de emprego, onde não há segunda chamada. Tal como não há segunda chamada em acidentes de trabalho, em competições, etc.

Quando se invocam os alunos prejudicados por uma ansiedade tóxica, esquecem-se os casos opostos (que veremos abaixo serem aos milhares): alunos que nos últimos 22 anos conseguiram em exame 5 valores ou mais do que tiveram na classificação interna. Um aluno com média de 19 em exame e 14 de classificação interna, não entra em nenhum curso de medicina quando muito poucos dos seus colegas que entram mostraram em exame saber tanto como ele.

Propriedade 3. Autocorreção de observações não representativas.

Se um aluno está doente no teste do 2.º período do 11.º ano e, por isso, teve 10, quando habitualmente tem classificações muito superiores, deve poder corrigir. Talvez algum professor dê segunda oportunidade ao aluno que teve um dia não no 1º teste do 2º período do 11º ano, mas não dá segunda hipótese ao aluno que andou perdido no 10º e 11º. Ele pode ter 20 valores em todos os exames do 12º, ser o melhor aluno de Portugal, mas sofrerá os estragos feitos na média nos dois anos anteriores. E todos os professores conhecem muitos alunos destes distraídos ou imaturos, e só no 12.º acordaram, quando o mal já estava feito.

Para que o sistema auto-corrija observações não representativas, a classificação de acesso deve ser a melhor de várias opções e não um caminho só, ou a decisão excruciante de ter de em algum momento “anular matrícula”. Se se aplica um exame com matéria de todo o secundário e o aluno tem 20 valores, que razão há para o amarrar ao 13 que teve no 10º ano ou ao 14 que o professor lhe deu na nota interna?

Exemplo alternativo: o IB

O IB — International Baccalaureate é um sistema internacional de ensino secundário, promovido e financiado pela UNESCO a partir de 1952, contando com o apoio inicial de Harvard e Oxford, e desenhado para ser tão bom como o melhor sistema nacional. É lecionado em várias escolas de Portugal. A classificação final tem normalização estatística e depende de duas componentes:

a) uma classificação interna com peso de 20% a 30% na nota final, resultante de avaliações feitas com regras de organização e de correção muito precisas, e com auditoria externa (correção por amostragem feita por professores estrangeiros);

b)  classificação do exame no final do secundário e correção externa;

Este sistema, embora não seja perfeito, evita várias injustiças presentes no sistema português.

O sistema americano

Ultimamente, várias pessoas têm proposto um sistema análogo ao americano em que se tem em conta várias componentes: classificação em teste standardizado (SAT) junto com a classificação interna da escola, entrevista, carta de motivação, cartas de recomendação de professores, prestação desportiva, artística, atividades extra-curriculares, etc., sendo que no fundo cada universidade define os seus critérios e admite quem quer.

Neste sistema, o mesmo aluno pode ser rejeitado numa universidade fraca e aceite na melhor; ou pode ser rejeitado pelas classificações da escola primária ou por ter cartas de recomendação frouxas, o que evidentemente não é culpa sua; dificilmente um aluno fica fora da universidade já que há imensa oferta e uma enorme competição entre elas, que fazem também políticas muito agressivas de recrutamento de estudantes no estrangeiro; para se candidatar, um aluno tem de estudar, pagar e seguir vários sistemas de acesso e candidatura; alunos muito ricos (com pais potenciais doadores da universidade) têm uma porta de entrada própria, etc.; pode ainda o melhor aluno da escola ser rejeitado numa universidade a favor de um colega muito pior, mas que é um desportista promissor, ou cumpre uma de mil quotas. (Como o sistema é muito discricionário, existe uma indústria de análise estatística às admissões e consequente acusação de que a universidade X discrimina a minoria Y, o que força os responsáveis a criar quotas e mais quotas).

Nos últimos tempos tem havido uma tendência para acabar com o exame standardizado (por, alegadamente, favorecer os filhos dos ricos que podem pagar preparação extra), mas o sistema alternativo sem exame está a favorecer ainda mais os ricos que podem pagar excecionais cartas de motivação e recomendação, sessões de preparação para entrevistas, ginásios de alto rendimento, etc.

O facto de tal sistema estar em uso nos EUA não significa que seja mais justo ou desejável, nem significa que os próprios americanos estejam felizes com ele. Envolvendo tantas componentes subjetivas, não se percebe bem que valores estão a ser preservados e que níveis de corrupção proporcionariam em Portugal. Além disso, os alunos não estão a correr na mesma prova, um aluno que sabe menos que outros pode ficar com a vaga por quotas ou por ser desportista, e quando as universidades de topo (com taxas de rejeição superiores a 95%) têm de desempatar candidatos excecionais, podem usar as notas que o aluno teve 10 anos antes de entrar na faculdade o que mata qualquer autocorreção do sistema.

Em qualquer caso, quando a rede de ensino superior é radicalmente diferente (as melhores universidades são privadas e livres de admitir quem entendem), importar para Portugal um tal sistema envolveria uma alteração radical de todo o sistema universitário português, não seria uma mera alteração nas regras de acesso. O sistema universitário português tem muito a aprender com o americano, mas o acesso não parece ser tal. Longe disso.

Número de vagas e subfinanciamento

As injustiças de acesso ao superior são também função do número de vagas, um valor definido pelo Governo, e portanto importava saber porque há tão poucas. Por exemplo, é razoável mandar muitos portugueses financiar (com propinas anuais de 10 mil a 25 mil euros) universidades espanholas, húngaras ou checas, e com custos de deslocação de 800-1500 euros por mês, quando as universidades portuguesas se debatem com um terrível problema de subfinanciamento? E havendo uma terrível falta de professores em matemática (e outras disciplinas), como se percebe que as vagas no país estejam tão longe do número de professores que se reformam anualmente (em matemática são mais de 200 reformas/ano e há menos de 60 alunos nos mestrados profissionalizantes) enquanto as médias de entrada em cursos de matemática (dada a elevada procura e o reduzido número de vagas) estão em alguns casos acima de 18 valores?

A tabela seguinte talvez dê uma pista para estes e muitos outros problemas do ensino superior do país (falta de Prémios Nobel, falta de inovação disruptiva, etc.):

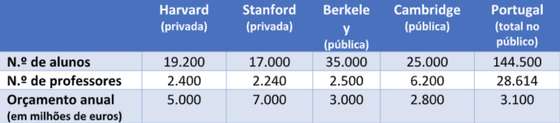
Aspetos a sublinhar

1. A régua que mede os conhecimentos dos alunos deve ser igual para todos e nesse campo o instrumento mais fiável é o exame nacional.
2. São precisos programas, metas e níveis bem definidos de forma a garantir que todos os alunos aprendem os mesmos conteúdos até ao mesmo nível de profundidade e, portanto, podem fazer exames em igualdade de circunstâncias, algo que não está a acontecer.
3. Os alunos que mostraram saber mais no instrumento de avaliação comum (o exame nacional) devem ter prioridade no acesso, o que não está a acontecer; poderemos ter até 30% dos alunos excluídos do curso que queriam ao serem ultrapassados por outros que mostraram saber menos.
4. Não é aceitável alunos de anos diferentes terem vantagem só por um exame ser mais fácil, por vezes muito mais fácil, pelo que as notas têm de ser trabalhadas estatisticamente.
5. Há claras assimetrias regionais no acesso a escola de qualidade que depois se tentam compensar com notas internas desproporcionadamente altas.
6. É preciso ter em conta que alguns alunos amadurecem mais tarde e não é justo cravar-lhes uma nota muito baixa logo no 10.º ano ou 11.º.
7. Precisamente por isso, há sistemas de ensino em que a nota de acesso só é definida em véspera de acesso ao ensino superior de forma a fotografar o que o aluno de facto sabe quando interessa e não o que sabia dois anos antes.
8. Os alunos com ansiedade tóxica precisam de acompanhamento profissional e existem milhares de alunos com o problema oposto: conseguem em exame muito melhor nota do que tiveram internamente, uma injustiça com impacto no seu futuro.
9. O maior diferencial, de longe, ocorre nas notas mais baixas, nos alunos que não pensam ir para o superior; isto significa que se o exame final deixar de contar para efeitos de conclusão do secundário, esse diploma ficará sem valor e os professores terão imensa dificuldade em conseguir a atenção, dedicação e trabalho destes alunos; na verdade, o secundário será uma tortura para professores e uma perda de tempo para muitos alunos, e as passagens serão virtualmente administrativas (os dados atuais, com imensos alunos a ter 10 de nota interna e 2 ou 3 valores em exame, são eloquentes).
10. Como país, temos de pensar muito seriamente se faz sentido mandar anualmente centenas de alunos pagar milhares de euros a universidades estrangeiras, quando as portuguesas se debatem com um terrível problema de subfinanciamento.
11. Como país temos de pensar o que significa 14 universidades públicas e 15 politécnicos terem no conjunto um financiamento muito inferior ao de uma pequena universidade americana ou inglesa.
12. A qualidade à saída da universidade é função da qualidade à entrada. Portanto, devem ser as universidades a definir os requisitos de entrada (e possivelmente a elaborar os exames nacionais de acesso ao superior). Ao básico/secundário cabe organizar-se para atingir os requisitos definidos. Observe-se que quando os alunos à entrada da faculdade não estão à altura do que se exige para uma saída de qualidade, ou fica perigoso usar os elevadores dos novos engenheiros e ser consultado pelos novos médicos, ou a mudança para o superior será um terror tal mudança de ritmo, quantidade de matéria e grau de exigência. A opção mais sensata é definir claramente o objetivo final e dosear o esforço ao longo dos 12 anos de escolaridade com vista a que tanto o básico/secundário como a transição para o superior decorram suavemente.
13. A conclusão do secundário precisa necessariamente de uma avaliação externa, mas que não tem de necessariamente coincidir com o exame de acesso ao superior.

As observações acima são um sumário da análise feita sobre os dados que estão (ou já estiveram) disponíveis no site da Direção Geral da Educação. Só consideramos os exames de primeira fase, para ingresso e para aprovação. Excluíram-se os exames para melhoria de nota e não se consideraram os exames dos alunos externos, pois não possuem classificação interna. É certo que abaixo fornecemos alguns desses dados, mas o verdadeiro objetivo deste artigo é sugerir-lhe que use o site Ranking Escolas para formular e testar conjeturas, aplicando com comodidade os filtros mais diversos. A série termina em 2019 porque para o ano de 2020 não foram disponibilizadas as classificações internas, e os resultados do ano 2021 ainda não foram libertados pela Direção Geral do Ensino.

Ultrapassagens

Os dados disponíveis implicam que no acesso ao superior há muitos alunos ultrapassados por colegas que mostraram em exame saber menos, mas beneficiaram de uma nota interna generosa; contudo, não é automático que isso prejudique alguém. Por exemplo, se um curso tem 20 vagas e apenas 15 candidatos, o diferencial pode alterar a ordem pela qual são colocados, mas todos entram. Em contrapartida, num curso com 20 vagas e 100 candidatos, no limite, os 20 candidatos que tiveram as 20 melhores notas em exame podem ser excluídos.

O que acontece exatamente? Para responder a esta questão há que saber a ordenação das prioridades de cada aluno, dado na posse do Estado. Em nome da transparência e justiça, o Estado devia divulgar anualmente o número de candidatos injustamente arredados da primeira opção, da segunda opção, ou que ficaram mesmo fora do ensino superior, devido a ultrapassagens conseguidas por alunos que mostraram em exame saber menos.

Com os dados públicos, só podemos tentar estimar a magnitude do problema. Para tal fizemos o seguinte exercício: vamos variando as vagas para os cursos com apenas um determinado exame específico; supondo que os melhores alunos em exame queriam ir para esses cursos, quantos ficariam excluídos ao serem ultrapassados pelo bónus resultante do diferencial?

Esta pergunta foi feita relativamente a cada um dos seguintes exames: Português, Matemática, Físico-Química, Biologia e Geologia.

Segue-se o número de alunos prejudicados pelas ultrapassagens em função do número de vagas, ou seja, alunos que se viram arredados da entrada num determinado curso por terem classificação interna inferior aos colegas que mostraram em exame saber menos.

Cursos com específica de Português:

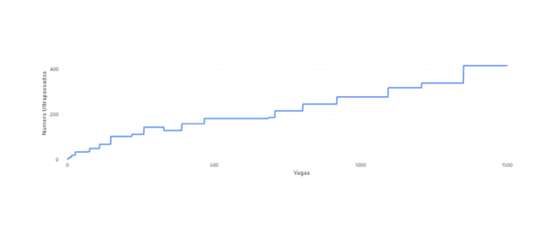
Figura 1 – Número de alunos excluído ao serem ultrapassados por quem mostrou saber menos num curso com específica única de Português

Em torno das 300 vagas há uma diminuição dos alunos injustamente ultrapassados pois o aumento de vagas faz com que alunos anteriormente não colocados, o sejam, deixando de ser contabilizados nas vítimas de injustiça.

A função tem um comportamento errático, mas de tendência marcadamente crescente. Evidentemente, se as vagas continuarem a crescer, o número de injustiçados começará a diminuir, acabando por chegar a zero (se todos os alunos fossem colocados na primeira opção ninguém seria prejudicado).

Cursos com específica de Matemática:

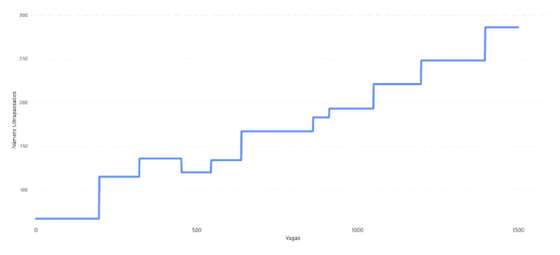
Figura 2 — Número de alunos excluído ao serem ultrapassados por quem mostrou saber menos num curso com específica única de Matemática

Cursos com específica de Físico-Química:

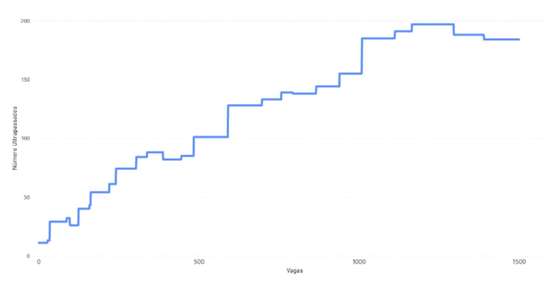
Figura 3 — Número de alunos excluído ao serem ultrapassados por quem mostrou saber menos num curso com específica única de Física e Química

Cursos com específica de Biologia e Geologia:

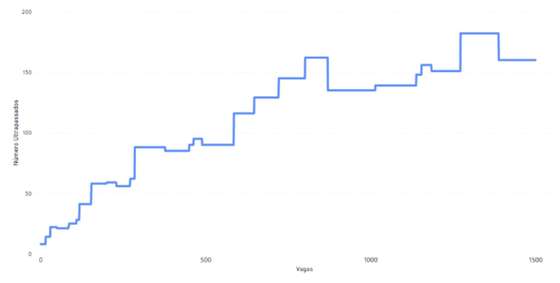
Figura 4 — Número de alunos excluído ao serem ultrapassados por quem mostrou saber menos num curso com específica única de Biologia e Geologia

Em todos estes exames, o número de alunos injustamente excluídos do curso por via do diferencial de notas ficou entre os 10% e 30%. Isto significa, por exemplo, que nos 1400 alunos que entram em medicina todos os anos, cerca de 180 alunos sabem mais, mas ficam fora, em benefício de 180 que entraram mostrando em exame saber menos. A exclusão é o caso mais dramático, mas considerações iguais se podem fazer sobre quem entra, mas não no curso perto de casa, etc.

Sabendo que está em causa a definição da vida da pessoa, uma única ultrapassagem injusta já seria uma tragédia nacional. Mas, como indicia a análise acima, as tragédias com nome próprio e Cartão de Cidadão deverão ser na casa dos milhares todos os anos e esse valor, que o Estado conhece com precisão, deve ser divulgado.

Os Exames

Começamos por dar uma visão da ordem de magnitude do problema do diferencial. A azul-claro está a evolução anual do número de exames onde o diferencial é superior a 3 valores e a azul-escuro o número de exames onde o diferencial é inferior a 1 valor.

Como se pode ver, os números são muito grandes, com dezenas de milhar de casos com benefício de um valor ou mais na nota de candidatura ao ensino superior, e largas dezenas de milhar de alunos com um benefício muito inferior ou nenhum benefício ou até a serem prejudicados. Existe uma tendência decrescente ao longo do tempo. Significará isso que as classificações internas se estão a aproximar da nota de exame ou deve-se a outras razões?

O gráfico, com os mesmos dados do anterior, mas em percentagem do número total de exames, talvez dê uma pista.

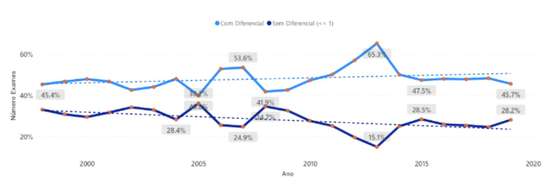
Figura 6 — Evolução anual da percentagem de exames por diferencial

A tendência decrescente observada anteriormente parece afinal resultar da diminuição do número total de exames.

Para analisarmos o impacto que o diferencial pode ter no acesso ao ensino superior, apresentam-se os mesmos gráficos, mas contabilizando apenas os exames com classificação positiva.

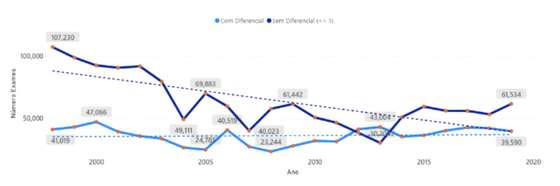
Figura 7 — Evolução anual do número de exames com classificação positiva e diferencial superior a 3 ou inferior a 1

Em 2019 o diferencial  superior a 3 valores estava em 40 mil exames. Segue-se a versão em percentagem destes dados.

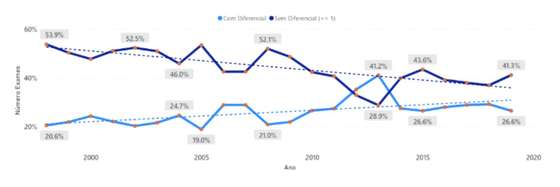
Figura 8 — Evolução anual da percentagem de exames, com classificação positiva, por diferencial

Verifica-se que, consistentemente, existe um benefício de pelo menos um valor na média de candidatura ao ensino superior para valores entre um quarto e um quinto dos casos.

O comportamento em 2006, 2007 e 2013 será explicável por exames com um grau de exigência mais elevado. Em sentido contrário, por exemplo, no ano de 2020, não representado no gráfico, a classificação mais observada, ou seja, a moda, no exame de matemática do 12.º ano foi de 19 valores; no ano seguinte foi 10 valores.

Vamos agora analisar a distribuição do diferencial.

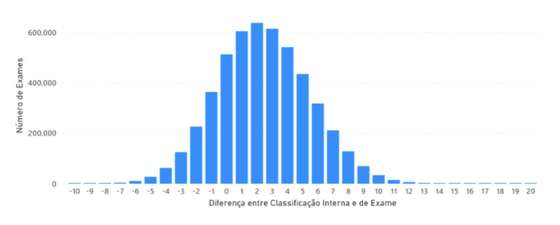
Figura 9 — Distribuição do diferencial no período de 1998 a 2019

O diferencial mais comum é de 2 valores, observado em mais de 600 mil exames, logo seguido do diferencial de 3 valores. Diferenciais superiores a 10 valores serão pontuais, possivelmente não valorizáveis. Claramente o diferencial positivo é muito mais frequente que o negativo, mas mesmo assim há um número significativo de exames onde os alunos conseguiram em exame mais 5, 6, 7 valores do que lhes foi dado pelo professor na classificação interna.

Repetimos o gráfico anterior, mas restrito aos exames com classificação positiva.

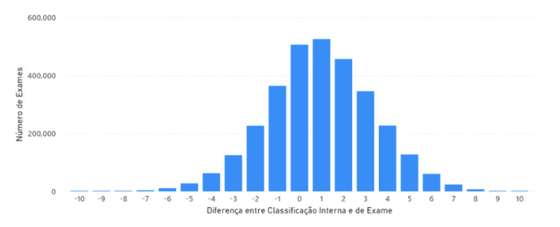
Figura 10 – Distribuição do diferencial no período de 1998 a 2019, apenas para exames com classificação positiva

Verifica-se que há muitas dezenas de milhar de alunos com diferencial superior a 5 valores, o que os beneficia em 2 valores ou mais na média de candidatura. Destacamos alguns casos extremos como por exemplo: houve alunos com 20 na classificação interna e 10 em exame. Talvez mais surpreendente, houve alunos com 10 de classificação interna e 19 em exame, ou 11 de classificação interna e 20 em exame.

Para ilustrar como o diferencial é um fenómeno de classificações baixas, apresentamos o gráfico seguinte onde para cada classificação de exame se fornece o número de exames com diferencial superior a 3 valores (linha a azul-claro) e o número de exames com diferencial inferior a 1 valor (linha a azul-escuro).

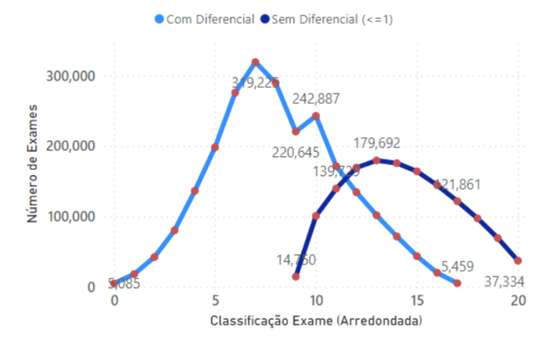
Figura 11 – Número de exames com diferencial superior a 3 valores e com diferencial inferior a 1 valor, por classificação de exame arredondada de exame, no período de 1998 a 2019

Por exemplo, no período em causa, houve 242.887 casos de classificação 10 em exame e nota interna igual ou superior a 13 na mesma disciplina. Já os 37.334 casos de 20 valores em exame, tiveram nota interna igual ou inferior a 20 valores (como não podia deixar de ser).

Faz-se o mesmo exercício do gráfico anterior, mas com a versão em percentagem.

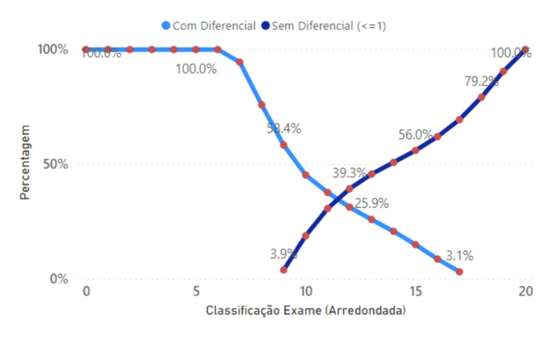
Figura 12 – Percentagem de exames com diferencial e sem diferencial, por classificação de exame arredondada, no período de 1998 a 2019

Com base nos dois gráficos anteriores podemos ver que no período em análise, existiram 242.887 alunos, 45.3%, com 10 valores em exame, mas com pelo menos 13 valores na classificação interna. Só no ano 2019 existiram 11.637 alunos (49.2%) nesta situação.

Também se constata, quanto maior é a classificação em exame, menor é a proporção dos alunos que tem diferencial superior a 3 valores. Mesmo assim, 14.9% dos exames com classificação de 15 valores, tiveram 18 valores ou mais de classificação interna nas mesmas disciplinas.

As Disciplinas

Vamos agora analisar como o diferencial superior a 3 valores se distribuiu pelas diversas disciplinas no período em análise. Na figura 9, a linha contínua indica os valores em percentagem do total de exames na disciplina. Neste gráfico apenas se consideraram as disciplinas atuais.

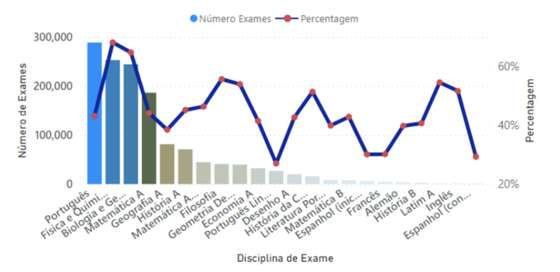
Figura 13 – Número de exames e respetiva percentagem, por disciplina, com o diferencial superior a 3 valores, no período de 1998 a 2019

Vamos considerar apenas os exames com classificação positiva:

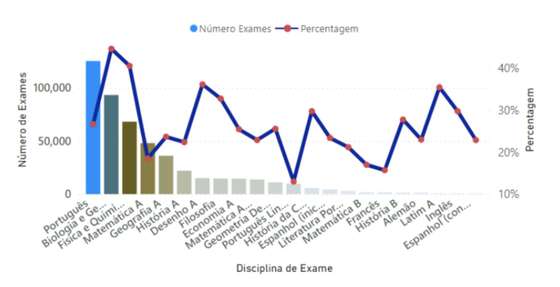
Figura 14 – Número de exames e respetiva percentagem, por disciplina, com exame positivo, com o diferencial superior a 3 valores, no período de 1998 a 2019

Como podemos verificar, a disciplina de Português apesar de ser a disciplina com mais exames com um diferencial superior a 3 valores, percentualmente é ultrapassada por várias disciplinas. As duas disciplinas com maior percentagem de exames com um diferencial elevado são as disciplinas de Biologia e Geologia e a disciplina de Física e Química A.

O gráfico seguinte dá uma ideia do diferencial médio por disciplina (apenas para exames com classificação positiva).

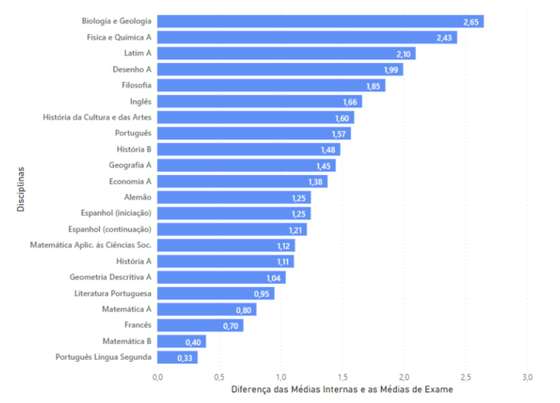
Figura 15 – Diferencial médio por disciplina, com exame positivo, no período de 1998 a 2019

Escolas/Agrupamentos

Vamos agora ver a evolução anual do número de escolas onde o diferencial foi superior a 3 valores. Por “escola” leia-se escola ou agrupamento.

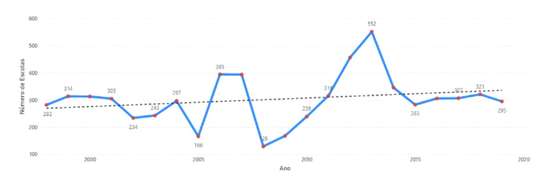
Figura 16– Evolução anual do número de escolas onde o diferencial foi superior a 3 valores

Note-se que em 1998 houve 282 escolas num total de 609 com diferencial superior a 3 valores, enquanto em 2013 foram 552 escolas de um total de 614. O que estes gráficos ilustram claramente é a flutuação no grau de dificuldade dos exames nacionais e a dificuldade que os professores têm em alinhar nota interna com nota de exame.

Repetimos o gráfico considerando apenas exames com classificação positiva.

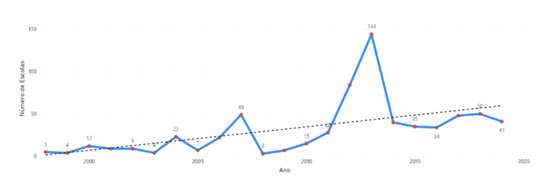
Figura 17– Evolução anual do número de escolas onde o diferencial foi superior a 3 valores nos exames com classificação positiva

Note-se a tendência crescente no número de escolas com diferencial médio superior a 3 valores. De sublinhar ainda a exigência dos exames de 2013 e 2007.

Escolas Públicas e Privadas

O próximo gráfico compara o diferencial, quando superior a 3 valores, nas escolas públicas e privadas.

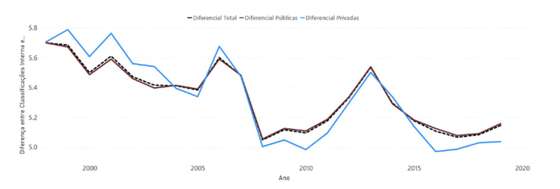
Figura 18 – Evolução anual do valor do diferencial, superior a 3 valores, nas escolas públicas e nas escolas privadas

Desde 2008, o diferencial nas escolas privadas é inferior ao das públicas, invertendo a tendência existente até à altura. Estamos a fazer a média de todos os exames de todos os alunos da escola.

As Regiões

Nesta secção iremos analisar a distribuição do diferencial pelas diversas regiões.

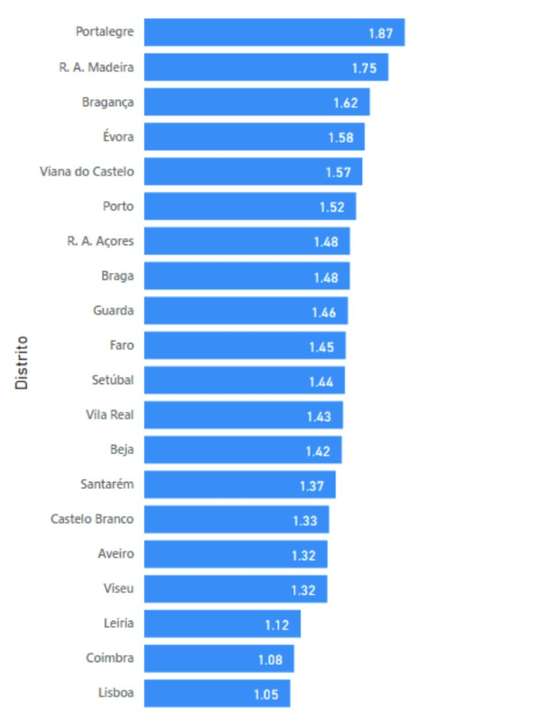
Figura 19  – Diferencial por distrito, para exames com classificação positiva, para o período de 1998 a 2019

Apresentamos a mesma análise ao nível dos concelhos.

Figura 20– Topo e base das escolas ordenadas por diferencial (apenas classificações positivas) no período 1998-2019

Existem 6 concelhos com escolas com um diferencial médio superior a 2.40 valores. Atente-se no caso do distrito de Leiria: há um concelho onde a média do diferencial é 2.72 e outro onde é 0.67. O aluno tipo do primeiro concelho tem um bónus de aproximadamente 0.9 valores na nota de candidatura enquanto o outro tem um bónus de 0.22 valores (é a diferença entre ter 17.8 ou 18.7, ou seja, não entrar em nenhum curso de medicina ou entrar em todos, quando o outro aluno, só por viver no concelho errado, passa de 17.8 para 18, ficando fora de qualquer curso de medicina).

A tabela seguinte refere-se a 2019 e tem a lista ordenada dos distritos por média em exame, de todos os alunos em todas as disciplinas, tem também o número de escolas públicas e privadas em cada distrito.

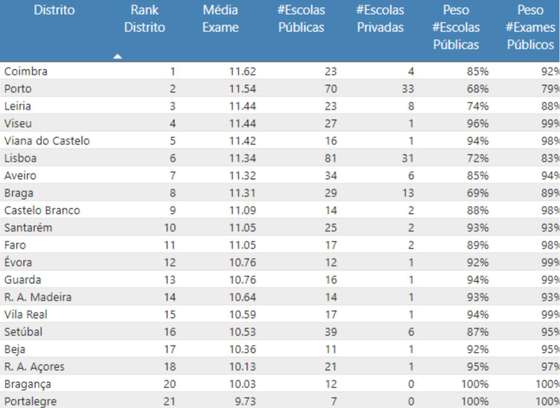
Observe-se que os dois distritos com maior diferencial médio no ano de 2019, Portalegre e Bragança, não tinham escolas privadas.

Há distritos com grande peso de escolas públicas, Viseu, Viana do Castelo ou até Coimbra, e média em exame muito alta (ou seja, alunos comparativamente bem preparados) enquanto em outros distritos, Portalegre e Bragança, o peso do público é de 100%, mas os resultados são mais pobres. O acesso a uma escola pública de qualidade tem, portanto, assimetrias regionais claras e isso talvez devesse fazer o Estado abrir os cordões à bolsa da educação no interior.

Masculino/Feminino

Analisamos agora a evolução anual do diferencial dos exames masculinos e femininos (apenas exames com classificação positiva).

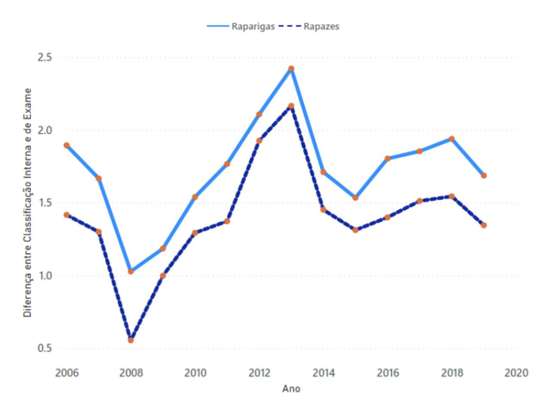
Figura 21 – Evolução do diferencial médio anual por sexo, para exames com classificação positiva

A diferença é consistente e significativa. Que explicação há para esta constatação? Os rapazes são mais vítimas de notas internas injustas? Reagem melhor aos exames?

O diferencial negativo

Temos olhado para os exames em que os alunos conseguiram melhor classificação interna do que conseguiram em exame. Vamos agora ver o caso oposto, analisando o diferencial médio por escalão de classificação de exame (classificação arredondada à unidade).

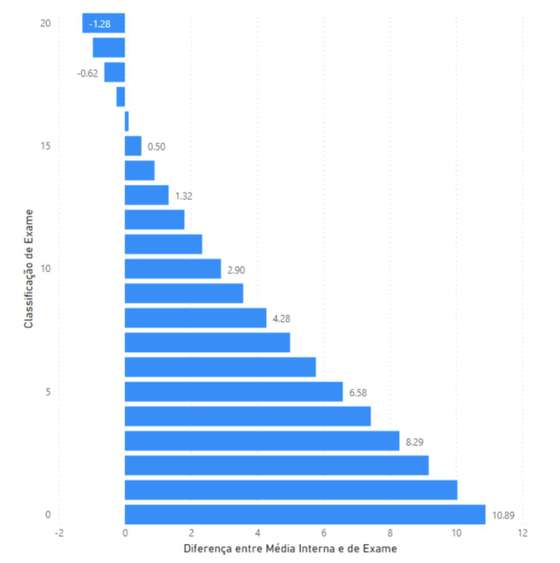
Figura 22 – Diferencial por escalão de classificação (classificação arredondada à unidade) de exame para o período de 1998 a 2019

Como se pode ver, as classificações de exame de 17 a 20, apresentaram neste período um diferencial negativo, ou seja, em média estes casos tiveram classificações internas inferiores ao que conseguem em exame, como seria previsível. Por exemplo, foi 18.72 a média interna de todos os alunos que conseguiram 20 valores em exame no período em análise.

No próximo gráfico analisamos a distribuição do diferencial.

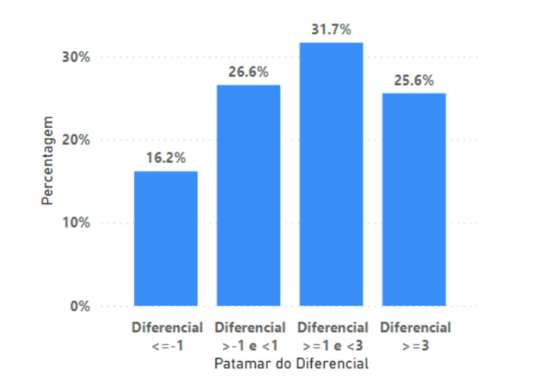
Figura 23 – Distribuição do Diferencial no período de 1998 a 2019, para os exames com classificação positiva

Constata-se que em 16.2% dos exames, os alunos conseguiram muito melhor nota em exame do que internamente. No extremo oposto, 26% tiveram internamente três valores ou mais acima do que conseguiram em exame.

Vamos agora ver como variou ao longo dos anos o máximo diferencial negativo.

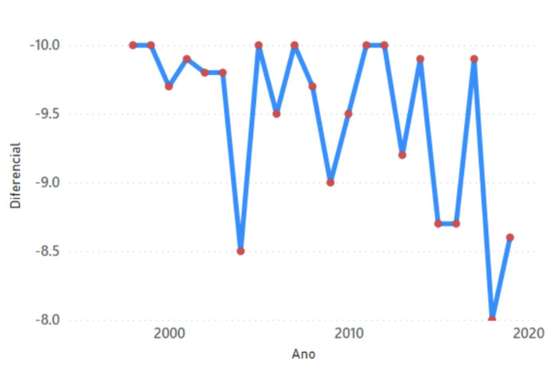
Figura 24 – Evolução do máximo diferencial negativo, no período de 1998 a 2019

Em 2019 o máximo diferencial negativo foi de 8.6 valores: alunos com 10 valores na classificação interna e 18.6 em exame. No período 1998-2019 houve seis anos em que alunos com classificação interna de 10 valores conseguiram obter 20 no exame da respetiva disciplina.

O próximo gráfico ilustra o número de exames em que o diferencial negativo foi superior a 5 valores o que pode corresponder a quase menos 2 valores na nota de candidatura ao ensino superior.

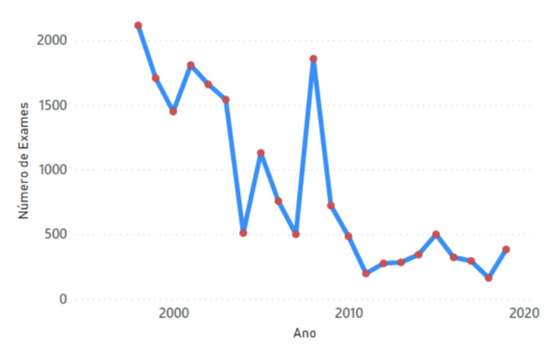
Figura 25 – Evolução anual do número de exames onde o diferencial negativo foi superior a 5 valores

De 1998 a 2019 houve um total de 18.988 exames com diferencial negativo superior a 5 valores. Há, no entanto, uma tendência decrescente destes casos. Não obstante, estamos a falar de centenas de alunos cuja nota de candidatura sofre um corte de 2 valores.

Vamos agora ver a evolução anual do número de escolas com diferencial negativo.

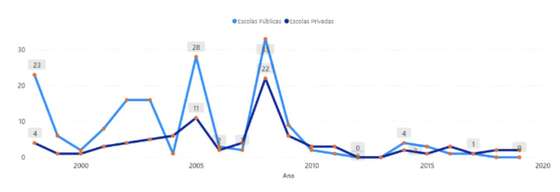
Figura 26 – Evolução anual do número de escolas com diferencial negativo para os exames com classificação positiva

Desde 2010 que se reduziu bastante o número de escolas com média interna inferior à média de exame. Observe-se também que, havendo uma escola privada por cada três públicas, proporcionalmente o diferencial negativo é muito mais prevalecente no privado do que no público.

A parte mais importante deste artigo não são estes dados e gráficos: é a possibilidade que lhe oferecemos de formular e testar as suas próprias conjeturas no site Ranking Escolas.

João Araújo é presidente da Sociedade Portuguesa de Matemática

Samuel Faria é gestor