Nos primeiros tempos em que me comecei a debruçar sobre, vamos chamar-lhes “primeiros princípios” da Economia, dei logo com uma realidade estranha. Todos os gráficos que me mostravam eram “conceptuais”. O que quero dizer com isto é que nenhum tinha valores nos eixos e as curvas eram meramente indicativas. Na verdade, nenhum dos gráficos que nos são mostrados correspondem a algo que seja demonstrável empiricamente. Para mim, se calhar mais do que para a esmagadora maioria dos economistas, tal não traz nenhum problema. Como sempre referi, prefiro sempre uma boa teoria a ser enganado pelos dados. Mas os gráficos revelavam outra coisa, a ignorância daquilo que se passa nos limites do sistema e que depois gera aquela sensação “mas há alguma coisa em que os economistas concordem todos?”.

Para mostrar a influência dos limites, vejamos aquilo que nos aparece normalmente como a explicação das poucas leis que os economistas assumem como verdade entre eles, a lei da oferta e da procura. O gráfico que nos aparece nos manuais de Economia é qualquer coisa como a figura da esquerda (*):

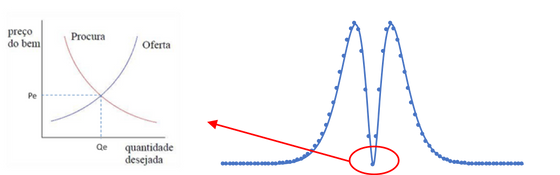
Mas num dos poucos sistemas onde se consegue medir as ordens de oferta e de procura, nos mercados organizados como as bolsas de valores, o gráfico real é similar ao que se representa à direita. O que os economistas nos dão é qualquer coisa na vizinhança do que chamam de ponto de equilíbrio (que não é equilíbrio nenhum, mas vamos deixar assim). Aquilo que se passa à medida que nos afastamos do ponto de equilíbrio, tal como a forma das curvas na sua vizinhança, é governado por princípios físicos que vamos chamar, a bem do entendimento, de leis “o que tem que ser, tem muita força”.  Por exemplo, o facto de todos morrermos um dia e a idade ser a principal causa de morte são as duas leis deste tipo que servem como base ao cálculo dos seguros de vida. Não sabemos como a nossa vida vai ser, mas sabemos que vamos morrer um dia de certeza absoluta. E com a morte podemos determinar a forma da curva que nos define a probabilidade de morrermos ao longo da vida. São os limites do sistema que a determinam, mais que o “meio”.

Voltando à oferta e procura, a curva da direita é relativamente óbvia se pensarmos que o número de agentes económicos é finito. Sendo finito, o número de ordens não pode ser infinito, pelo que a curva tem que ir para zero nalgum ponto, para além do ponto de equilíbrio. Pela lógica, se temos um ponto positivo onde é mínimo e um ponto onde é zero, a linha tem que ter um máximo finito maior que esse mínimo. E, “lo and behold”, eis a curva da oferta e da procura teoricamente estabelecida, e empiricamente confirmada, representada à direita. Sem querer ser demasiado aborrecido, a forma das “barrigas” das curvas da figura da esquerda deriva diretamente do pressuposto de que “tem que ir a zero”. O interessante é que a curva da esquerda, aquela que é ensinada nos primeiros anos de Economia, é quase (ver a nota) uma derivação da curva da direita numa vizinhança próxima do ponto de equilíbrio, que é o domínio de trabalho dos economistas. Mais uma vez, a sua forma é determinada pelo que se passa nos limites do sistema, embora a “física” toda se passe no ponto de equilíbrio onde a trocas ocorrem de facto. Giro, não é?

Esta reflexão apareceu-me quando se começaram a ouvir as notícias do resgate das crianças da Tailândia, presas numa gruta nas profundezas da terra. E a questão que tenho é: quanto vale economicamente cada uma daquelas vidas?  Sim, a pergunta é de uma brutalidade a roçar o absurdo. E não, não estou a tentar quantificar cada uma daquelas vidas. Mas é uma reflexão importante e que se prende com os esforços que estamos dispostos a fazer, os sacrifícios que estamos dispostos a fazer para proteger cada um de nós.

E porquê? Se formos pegar nas despesas que os tailandeses incorreram, dividíssemos por doze e apurássemos um valor por pessoa, podemos dizer que isso, multiplicado por 68 milhões, seria aquilo que estariam dispostos a pagar para salvar a população inteira? A questão é lícita se estivermos a discutir um orçamento para a saúde ou para a segurança. Mas façamos a pergunta ao contrário, se gastassem isso, multiplicado por 68 milhões, na saúde, salvavam mais doze pessoas do que aquelas que o sistema de saúde tailandês salva hoje? Disso acho que não temos grandes dúvidas, muito mais do que doze. Então o que estes doze valem menos do que os doze que ficaram presos na gruta?

Vamos mais uma vez olhar para os limites do sistema usando uma regra do tipo “o que tem que ser, tem muita força”. A verdade é que os orçamentos não são ilimitados, porque os seres humanos e o trabalho que produzem também não o são. Embora esta afirmação em si mesma possa ser uma desilusão para a esquerda radical, a verdade é que é assim. Agora, em vez de irmos aos limites superiores do sistema vamos aos inferiores, a cada uma das pessoas com cara, nome, pai, mãe e clube de futebol. Quer o leitor atirar um número para a vida do seu filho? Não, claro que não. Nem consegue imaginar que número vai atirar e já está a ficar irritado comigo por todas as razões racionais e religiosas. Então, eu vou atirar um valor pensando em cada um dos meus filhos: é infinito. E cada um dos pais tailandeses que acompanharam o resgate pensou a mesma coisa; gastem o que for preciso, movam céus e mares, mas o meu filho vai ter que sair vivo daquela gruta. E todos os tailandeses decidiram que assim seria. Mas isso não é matematicamente impossível? Não.

Na verdade, o valor de cada um pode ser infinito desde que o valor de todos (leia-se infinito) seja zero. E isso é possível? Claro que sim.  Vejamos a curva da figura em baixo. Pegando apenas nos limites do sistema, o que tem que ser é que o valor de cada um seja infinito (extremo esquerdo do gráfico) o que dá que o valor de todos no infinito (extremo direito do gráfico) seja zero.

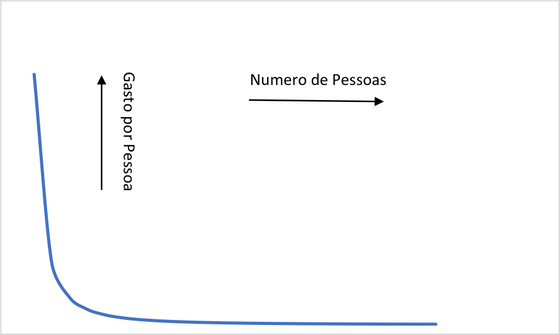
Então e porque é que a curva tem uma “barriga” daquelas? Porque impusemos que o orçamento teria que ser finito (a justificação matemática era mesmo chata, pelo que ficamos assim).

A conclusão é que cada uma das vidas dos nossos filhos não tem valor finito, porque cada um de nós assim o impôs. Podemos, então, concordar com os dogmas religiosos e sociais inscritos na nossa memória estática, e na nossa memória coletiva, de que a vida não tem valor. Mas cada uma das vidas humanas, tem, quando a humanidade é vista no seu todo. É isso que nos obriga a viver em Estados que usam a economia coletiva para proteger cada um de nós e todos simultaneamente.

Temo com isto desiludir os mais liberais dos leitores. Sim, um Estado que proteja a vida (leia-se segurança social/física e saúde) não só é importante como não é sequer discutível do ponto de vista matemático, se tomarmos como infinito o valor da vida dos seus filhos. Por outro lado, como os ultra-liberais lusos são também profundamente religiosos, creio ter compensado a desilusão da necessidade de uma saúde pública com a infinitude do valor de cada vida. A todos, dos liberais aos marxistas radicais, um grande obrigado porque no dia em que realmente um dos meus filhos precisou desse valor infinito, estiveram todos lá na pessoa dos profissionais que vocês pagam com o vosso trabalho. Como tenho a certeza de que se os pais tailandeses precisassem de nós, nós lá estaríamos.

 (*) Se a curvatura das curvas da esquerda parece ao contrário, é porque os economistas metem ao contrário. Mas também metem sem curvatura… A imagem da esquerda foi tirada de um bloguecriado pelos alunos de Economia A, 10º e 11º anos, do Curso de Ciências Socioeconómicas, da Escola Secundária Camilo Castelo Branco, de V. N. Famalicão, em 2011, não encontrei o(s) nome(s) do(s) professor(es). São tão melhores que nós quando os professores resolvem ser profissionais, não são?

(As opiniões expressas neste artigo são pessoais e vinculam apenas e somente o seu autor)
PhD em Física, Co-Fundador da Closer, Vice-Presidente da Data Science Portuguese Association