A cena é uma sala mal iluminada por uma lâmpada branca crua. Paredes encardidas e chão riscado. Uma mesa com pernas desequilibradas e uma cadeira dura. Um homem mal dormido e desesperado por um cigarro espera que chegue um detetive da PJ para lhe fazer a pergunta a que ele não quer responder: quem é que assaltou a velhinha? Ele resiste. Quando tinha falado com o companheiro na véspera, antes do assalto, tinham combinado que não diziam nada se fossem apanhados. Mas o PJ é simpático, atencioso, propõe um negócio irrecusável, se confessar antes do outro leva só um ano de cadeia mas se o outro confessar antes leva dez anos
Todas as semanas esta cena é recriada em livros, na televisão, no cinema. E em todas as vezes os aficionados de policiais ficam em “suspense”. Mas John Nash não teria ficado.
John Nash, que morreu no sábado passado, era um matemático americano que contribuiu para o desenvolvimento da disciplina de Teoria dos Jogos, formalizada no final dos anos quarenta por John von Neumann e Oskar Morgenstern na publicação Theory of Games and Economic Behaviour.
A Teoria dos Jogos apareceu como uma resposta sistemática e coerente a problemas de interação estratégica que tinham sido estudados desde sempre pela humanidade, em estratégias militares, na vida empresarial ou nas relações pessoais. O desenvolvimento destes modelos respondia aos problemas levantados pelo facto de as ações dos diferentes agentes serem afetadas pelas decisões de outros agentes, muitas vezes não tratadas nos modelos económicos clássicos.
No campo da economia, o estudo das interações estratégicas começou com Augustin Cournot, em 1838, e o seu trabalho sobre qual a produção de equilíbrio numa situação de duopólio, isto é situações em que existem dois produtores que satisfazem toda a procura. Hoje em dia reconhece-se que o equilíbrio de Cournot é uma forma de equilíbrio de Nash.
Um dos principais contributos de Nash para a Economia vem da sua tese de doutoramento em Princeton em 1950, em que Nash complementa a obra de von Neumann e Morgenstern, por sinal a única referência bibliográfica da tese para além de uma publicação do próprio Nash. Na sua tese, ele distingue entre equilíbrios cooperativos e não cooperativos, isto é, os que dependem da possibilidade ou impossibilidade de fazer coligações, de comunicar ou de fazer pagamentos fora do jogo, e define um equilíbrio como uma situação em que nenhum dos jogadores, sabendo a estratégia do outro, que está fixada, tem incentivos para mudar a sua decisão. Noutros termos, se os jogadores se encontrarem num equilíbrio de Nash, não têm motivos para alterar a sua estratégia.
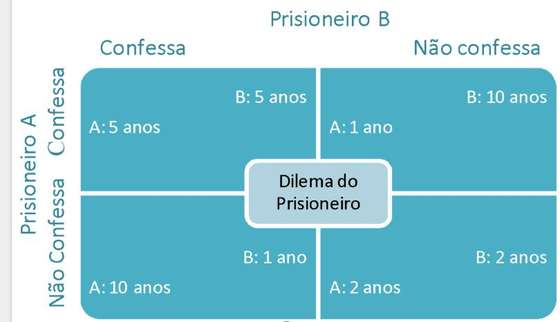
Por exemplo, retomando o exemplo acima (do assalto da velhinha), que ilustra o jogo chamado Dilema do Prisioneiro, o equilíbrio de Nash é a situação em que os dois confessam o crime. Se definirmos a punição em termos de anos de cadeia como sendo a matriz à direita, e partirmos do primeiro quadrante, onde os dois confessam, cada prisioneiro apanha cinco anos de cadeia. Nesse quadrante, não existe incentivo para desviar. Por exemplo, se A confessar e B não confessar, então B leva 10 anos em vez de 5.
Este jogo tem também a particularidade de o equilíbrio de Nash não ser o melhor para os jogadores. A melhor decisão para ambos seria nenhum confessar, cada um levaria apenas 2 anos de cadeia, mas nesse ponto ambos têm incentivo a quebrar o acordo pelo que voltamos ao primeiro quadrante.
O equilíbrio de Nash para este jogo será sempre confessar, o que retiraria bastante emoção aos policiais, se não houvesse criatividade e licença artística.
Após uma década de enormes avanços na matemática e na economia Nash foi diagnosticado com esquizofrenia e passou várias temporadas em hospitais psiquiátricos, internado contra a sua vontade. No entanto, durante esse período, as 27 páginas da sua tese tiveram aplicações em variadíssimos ramos das ciências. Na economia, por exemplo, o seu equilíbrio foi aplicado nas interações empresariais, nomeadamente para estudar o comportamento dos oligopólios ou na utilização de redes de tráfego. Vários discípulos seus continuaram a melhorar a sua teoria original.
Inesperadamente e gradualmente, Nash conseguiu recuperar suficientemente para retomar, nos anos 80, contactos profissionais e receber, em 1994, o prémio Nobel. Em entrevistas ao longo dos anos adivinha-se que estava feliz por ter recebido este prémio mas também um pouco surpreendido, uma vez que considerava que o seu contributo para a Economia não tinha sido tão importante como para a Matemática.
Para além deste contributo, Nash também desenvolveu diversos trabalhos para a Teoria dos Jogos em estratégias de negociação. Mas o seu trabalho mais importante – e no qual trabalhou até ao fim dos seus dias, foi realizado nas equações diferenciais parciais. Felizmente teve a oportunidade de ver também o seu trabalho em Matemática reconhecido quando recebeu, há cinco dias atrás, o prémio Abel, equivalente do Nobel para a Matemática. John Nash morreu quando voltava de carro para casa depois de receber este prémio, aos 87 anos.