No dia 25 de novembro de 1915 Albert Einstein apresentou a fórmula definitiva da teoria da relatividade, introduzindo o misterioso conceito da curvatura espaço-tempo. O professor e físico da Universidade de Barcelona (ICREA), Roberto Emparan, aprofundou e ajudou a explicar as principais curiosidades sobre essa teoria em 10 perguntas.

O que é que se comemora exatamente no dia 25 de novembro de 2015?

Passaram exatamente 100 anos desde o dia em que Albert Einstein apresentou e explicou na Academia Prussiana de Ciências, em Berlim, as equações definitivas da teoria geral da relatividade. Depois de uma década de tentativas para conciliar a força gravitacional com a sua teoria da relatividade especial (1905) e do matemático David Hilbert andar atrás de Einstein, este finalmente deu uma forma precisa e definitiva à teoria que foi considerada como uma das principais da humanidade. A teoria foi publicada no mesmo dia, 25 de novembro de 1915, nas atas da academia.

Einstein apresentou nesse dia a equação como a conhecemos hoje?

Na verdade o sistema é composto por dez equações, mas pode ser escrito de forma unificada utilizando o símbolo “=” e resumi-lo em : R μν -1/2 g μν R = 8πG T μν. Na equação original, que Einstein escreveu no seu artigo, utilizou alguns símbolos em latim em vez de grego e distribuiu os termos de uma maneira um pouco diferente, ainda assim, ela é totalmente equivalente a esta.

PUB • CONTINUE A LER A SEGUIR

teoria

Einstein publicou a 25 de novembro de 1915 a equação da teoria da relatividade. Créditos: Atas da Academia Ciências em Berlim

E o que significa R μν -1/2 g μν R = 8πG T μν numa língua que todos possamos compreender?

Na linguagem comum, a equação de Einstein relaciona dois aspetos: a curvatura do espaço-tempo e massa (energia).
Isto é, uma massa – por exemplo a terra- cria um campo gravitacional, que por sua vez exerce uma força que controla o movimento de outras massas, desde uma simples maçã à lua. Com a contribuição de Einstein, a teoria de Newton foi substituída por uma outra que incluiu uma aproximação válida para massas e velocidades relativamente pequenas. Mas a teoria de Einstein era muito mais refinada do que a de Newton, já que mudou completamente o conceito do que é e como funciona a gravidade.

Quais são as diferenças entre a visão clássica do mundo de Newton e da relatividade de Einstein?

Existem duas diferenças essenciais. Por um lado, na fórmula de Einstein desaparece a noção de gravidade que foi substituída por algo mais misterioso: a curvatura do espaço-tempo. Por outro, a teoria da relatividade une numa só equação a duas leis básicas da teoria newtoniana. Sem dúvida alguma que a eliminação da gravidade como uma força “real” e a sua interpretação como um “efeito aparente” da curvatura do espaço-tempo é o elemento mais revolucionário da teoria.

Podemos representar o conceito da curvatura do espaço-tempo?

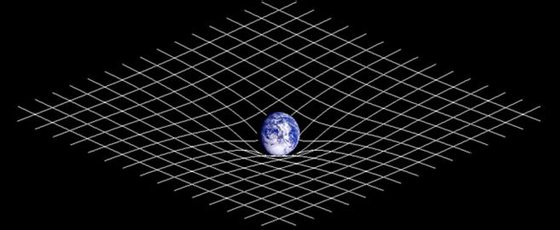
É habitual representar os seus efeitos através do exemplo de uma cama elástica (espécie de trampolim), que fica deformada com o peso de uma massa maior. Embora seja ilustrativa, esta analogia não consegue transmitir o essencial da curvatura espaço-tempo que dificilmente afeta as direções espaciais do trampolim, mas que ocorre principalmente no sentido do tempo. A teoria é demasiado rica e subtil para ser representada com imagens simplificadas.

teoria2

A representação da curvatura espaço-tempo numa cama elástica. Créditos: Wikipedia

Portanto, não há forma de representar numa única imagem a teoria da relatividade?

Seria necessário utilizar diferentes imagens para ilustrar diferentes aspetos da teoria, embora não exista nenhuma que consiga representar tudo corretamente. A ideia do trampolim é boa, mas tem limitações. Por exemplo, não consegue ilustrar nem mais ou menos o que é um buraco negro e cria confusões: como é que dizemos que a curvatura é tão pequena e que não a notamos habitualmente sendo, ainda assim, suficientemente grande para que uma concha ou a lua sigam uma trajetória curva ao invés de uma linha reta? Era necessário explicar porque é que nos movimentamos mais no tempo do que no espaço e o que é que isso implica.

O que relaciona a teoria da relatividade geral e os buracos negros?

Tudo começou em 1915. Numa carta fechada, em 22 de dezembro desse ano, o astrónomo alemão Karl Schwarzschild disse a Einstein que tinha encontrado uma solução extremamente simples para as suas equações. Concretamente para o caso da curvatura (o da gravidade) que cria corpos massivos como o Sol, Terra, estrelas e objetos que nenhum dos dois conheceu: os buracos negros.

Einstein acreditava em buracos negros?

A existência de buracos negros envolvia a teoria de um modo tão radical que nem sequer Einstein foi capaz de entendê-la. Só a aceitou depois, após um longo e árduo processo que ficou completo nos anos 60 e que provou que as melhorias teorias da física são aquelas que transcendem os seus próprios criadores. Sabemos agora que os buracos negros existem mesmo.

Por que é que os buracos negros também enfrentam a teoria da relatividade e a física quântica?

Imagine que deixa cair um telemóvel ou um tablet num buraco negro. Existe alguma possibilidade, ainda que remota, de recuperarmos a informação que tínhamos neles? A teoria de Einstein diz-nos que não: quando alguma coisa cruza o horizonte do buraco negro já não é possível receber mais nenhum sinal. No entanto, a física quântica diz-nos que a informação nunca pode ser perdida, mas que se pode misturar de uma maneira muito confusa, embora seja possível recuperá-la de alguma forma. Esta é a contradição entre as duas teorias, conhecida como o paradoxo da perda de informação em buracos negros.

A teoria da relatividade tem alguma aplicação prática?

Se alguém não estiver suficientemente impressionado pela teoria de Einstein e pela sua utilidade prática, basta então pensar num GPS. Se isso não levasse em conta o efeito, embora pequeno, que a curvatura do espaço-tempo tem sobre o aparelho (o GPS) que recebe o sinal de satélite, os nossos carros acabariam em poucos minutos longe do sítio certo. Assim, da próxima vez que o navegador GPS lhe diga “chegou ao destino” e não ao fundo de uma ravina ou contra uma parede, agradeça a Einstein.

Artigo Enrique Sacristán publicado pela Agencia Sinc. Texto original aqui.