Um exercício de matemática de um exame de liceu sobre duas moedas de 50 cêntimos está a colocar a internet a puxar pela cabeça. Os alunos consideraram-no difícil. Há muitos que discordam e que dão a solução. Outros concordam e nem tentam responder.
Acha que é capaz? (A solução está mais abaixo, por isso, não faça batota) Ora aqui está:
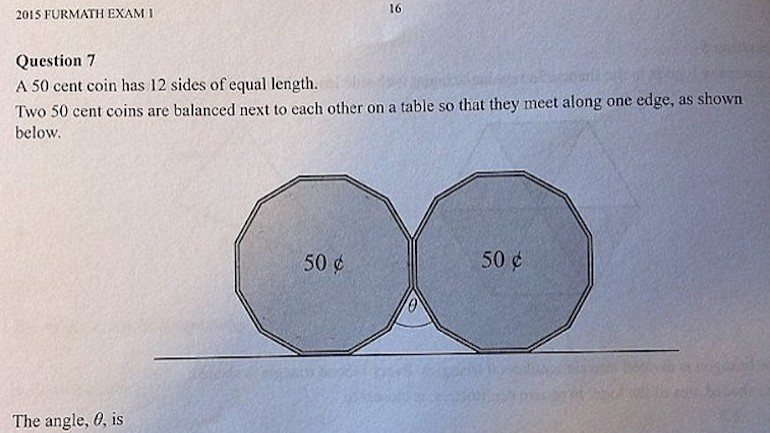
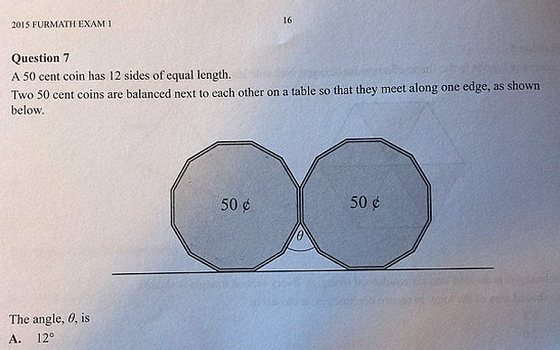
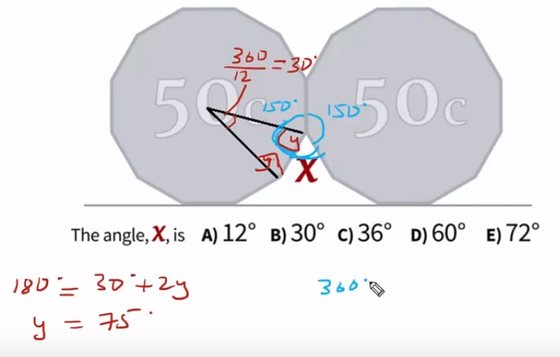
“Uma moeda de 50 cêntimos tem 12 lados com o comprimento igual. Duas moedas de 50 cêntimos estão equilibradas encostadas uma à outra.”
Este é o problema que se coloca. A seguir pede-se para descobrir qual é “o ângulo 0”. E sugerem-se as seguintes respostas: A. 12º; B. 30º; C. 36º; D. 60º; E. 72º
Em qual das respostas aposta? Escolha-a aqui e fique já a saber a resposta certa.
Veremos então porquê.
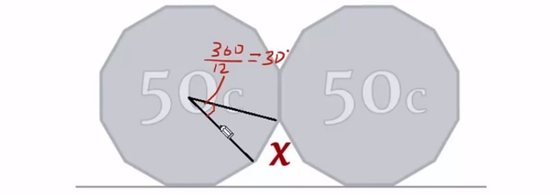
Concentre-se nos dados que a pergunta providencia. Sabemos que cada moeda tem doze lados iguais. Imagine então que a moeda tem um furo no meio a que vamos chamar “ponto X” e que a cada um dos vértices (pontas) dessta moeda tem o nome de uma letra. Ora, se todos os lados são iguais podemos formar doze triângulos se ligarmos o ponto X aos vértices A e B, C e D, e por aí adiante. E todos estes triângulos vão ser iguais entre si.
Vamos trabalhar apenas com o triângulo [XAB], isto é, com vértices no ponto central X e nos vértices A e B da moeda.
A soma de todos os ângulos internos de um triângulo é sempre igual a 180º. Então qual será o valor dos ângulos deste triângulo? Uma pergunta de cada vez: vamos calcular o valor do ângulo formado no ponto X entre os lados do triângulo. Sabemos que o ângulo de um círculo imaginário localizado no centro da moeda é de 360º. Para descobrir o valor do ângulo em X basta então dividir 360º pelo número de triângulos que podemos criar, que são 12. Conclusão: o valor do ângulo em X é de 30º.
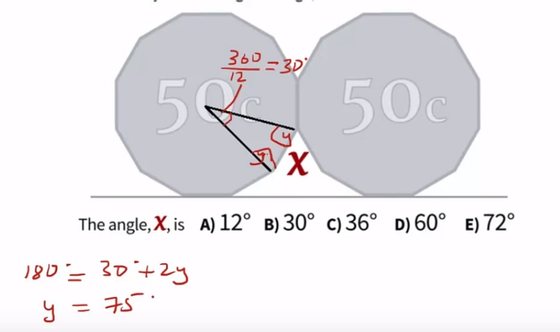
Agora que temos este valor descoberto, podemos partir para os outros ângulos. Mas para tal é preciso saber que este é um triângulo isósceles. Isso significa que dois dos seus lados são iguais e, sendo assim, dois dos seus ângulos também vão ser iguais. Ora, se subtrair os 30º do ângulo em X aos 180º formados pela soma de todos os ângulos do triângulo, vai saber se a soma dos dois ângulos que queremos agora descobrir é 150º. Se eles são iguais, basta dividir este valor por dois e saberemos que tanto o ângulo em A como o ângulo em B têm 75º.
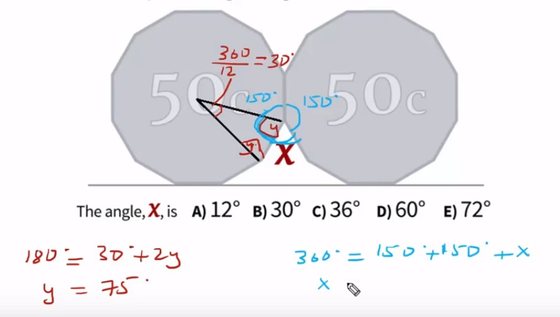
Mas porque é que isto é útil? Se as duas moedas são iguais, o processo de pensamento para uma e outra também são iguais. Se o triângulo [YAB] (sendo Y o ponto central da outra moeda) é igual ao triângulo [XAB], então os seus ângulos são iguais. Mas para descobrir o ângulo desconhecido é necessário ter noção que o ângulo formado em B no triângulo [YAB] é igual ao ângulo formado em B num outro triângulo [XBC]. Se calcularmos o valor da soma dos ângulos em B de ambos os triângulos conseguimos descobrir o ângulo dos vértices da moeda: a multiplicação por dois de 75º dá então 150º.
Vamos agora raciocinar. O valor do ângulo que queremos descobrir não passa da subtracção de 360º (o ângulo de um círculo imaginário com centro em B) pelo valor vértice de cada uma das moedas que coincidem. Se um dos vértices tem um ângulo de 150º, o outro terá valor igual e então a sua soma será 300º. Subtraindo 300º aos 360º desse círculo com ponto em B, chegaremos ao valor que queremos descobrir: 60º.
A resposta correta é, portanto, a D. 60º.