Numa das suas “experiências mentais”, Einstein imaginou uma pessoa a cair livremente sobre a Terra fechada dentro de um elevador. Imaginem estarem a subir de elevador e os cabos partirem-se. Se não conseguissem ver nada para fora e se não houvesse chão onde o elevador parar, quem vai lá dentro não sentiria a gravidade porque, quer o elevador, quer a pessoa, seriam sujeitos à mesma aceleração. A conclusão não poderia ser mais desconcertante: se a gravidade depende do observador, então a gravidade é uma “força aparente” e, logo, não existe.
Einstein, com base nesta conclusão desenvolve a mais brilhante peça de ciência produzida por um ser humano, completamente retirada da dedução lógica, mexendo-se entre matemática que não existia e sem saber se aquilo a que eventualmente chegasse poderia ser corroborado experimentalmente. Falo da Teoria da Relatividade Geral, a teoria que fez de Einstein, o “Einstein”, e que muito dificilmente surgirá de novo algo de tão fantástico na evolução do homem.
Aquilo que faz da Relatividade Geral uma teoria tão especial é o facto de questionar aquilo que é profundamente marcado na nossa intuição: a geometria. Em quase todo o conhecimento humano, das ciências mais duras, às mais “molinhas”, aquilo que tomamos como certo é que a geometria do espaço de fundo onde os fenómenos se observam não muda. Um metro aqui é um metro na China, conseguimos determinar a posição de um objeto em três dimensões e não esperamos que o espaço dependa do tempo. A mudança na geometria é algo com que a nossa intuição não lida muito bem, apesar de vivermos num universo que é exatamente isso, um sistema em que a geometria está sempre a mudar. A nossa intuição está treinada num local muito pequeno do espaço-tempo e nós, como a pessoa dentro do elevador, também estamos a mudar com o universo.
O que é que isto tem a ver com o vírus? Desde há um par de semanas que andamos a alternar entre especialistas de uma pandemia e uma pandemia de especialistas, a discutir números de um país para o outro baseado no mesmo princípio que falei atrás, de que a geometria do espaço em que o fenómeno se passa não se altera. Ora, numa propagação de um vírus, essa questão é particularmente importante. Vejamos o seguinte boneco
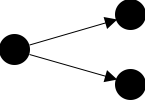
para representar a contaminação. As bolas representam pessoas e as setas representam transmissões. Até aqui é fácil, certo? Mas o que representa o fundo branco, aquele onde estas letras e a figura acima aparece impressa? Pois, o problema é esse. O fundo branco não existe porque o vírus não vai rua fora à procura de pessoas, ele precisa de viajar nas pessoas. Embora eu tenha feito as setas com comprimento suficiente para se perceber, o facto é que esse comprimento não existe para o vírus. Nem esse comprimento, nem o espaço em branco. Aquilo que eu fiz ao representar a propagação do vírus desta forma foi usar um espaço onde a minha intuição navega bem (chama-se espaço Euclidiano bidimensional), mas que para o vírus não existe. O que existe para o vírus são pessoas, sendo que todo o espaço para ele é composto de contacto entre pessoas. Ainda que estas se mexam num espaço bidimensional como é o nosso chão, o espaço para o vírus tem uma geometria completamente diferente. Esta é alterada no tempo conforme as pessoas são suscetíveis ou não a transportar o vírus. Se calçarem os sapatos do vírus, percebem que o mundo para ele tem uma matemática completamente diferente.
São estes os problemas que para nós, que vivemos toda a vida a aprender problemas em que tomamos como certa a invariância da geometria, são muito complicados de resolver porque (quase) toda a matemática que usamos confia nesse pressuposto de que medir um metro, aqui ou na China, é igual. Ora, como a propagação do vírus (ou a economia, ou a linguagem, ou a expansão do universo, …) é um sistema em que o fenómeno influencia a geometria do problema, aquela matemática que aprendemos que nunca falha resulta, habitualmente, num enorme disparate. E os primeiros objetos matemáticos a morrerem são os estatísticos.
Dentro destes disparates estão os estudos de contaminados por milhão de habitantes, de mortos desde as medidas governamentais, das próprias medidas governamentais, etc. Tudo depende da geometria do espaço que o vírus vê à sua frente e, como este a influencia e altera, o vírus vê no metro de Tóquio ou de Nova Iorque uma geometria completamente diferente daquela que vê no Sul da Líbia ou no interior do Arizona. Fazer médias por milhão de habitantes é uma asneira infantil, mas fazer contas desde que foram implementadas medidas, que não parece assim tão pateta, depende do rigor das medidas e de como foram cumpridas pela população. Repare-se que o Norte e o Sul de Portugal estavam sujeitos às mesmas medidas de contenção e, no entanto, “por milhão de habitantes” temos resultados muito diferentes.
Posto isto, conseguimos resolver o problema do ponto de vista matemático? Não vai ser fácil, e certamente não o conseguiremos em tempo útil para usar nesta pandemia. Uma boa parte da investigação que vai sair desta crise vai ser a tentativa de conseguir reproduzir a geometria vista pelo vírus (algo que está a ser feito, por exemplo, em conjunto pela Closer Consultoria, o Centro de Física Teórica e Computacional da Faculdade de Ciências de Lisboa e a NOS Comunicações) para compreendermos como as medidas governamentais conseguiram alterar o espaço, e como estas alterações geométricas se refletem nas medidas numéricas que tiramos. Haverá, decerto, outras equipas por esse mundo fora que estarão a fazer outras abordagens. O fundamental a entender não é se a matemática da propagação está correta, essa sabemos há 200 anos. Importa, sim, entender como as alterações induzidas à geometria do espaço visto pelo vírus influencia essa matemática já que, acreditamos nós, não haverá muitas mais oportunidades para o fazer.
A importância de se entender como se induzem essas alterações de geometria será clara na próxima vez que se tomarem medidas de confinamento, medidas essas que foram tomadas, não porque não se conheça a matemática da propagação em pandemias, mas porque o problema não era esse. Não me canso de repetir que o problema do Covid-19 não era um problema científico ou da matemática da pandemia. Trata-se de um problema de engenharia do sistema público de saúde que está desenhado para um nível de resposta que não era adequado à gravidade dos efeitos deste vírus. A única forma de responder a este problema de engenharia era induzir alterações na geometria do espaço do vírus. A questão é que isso foi feito de forma meio atabalhoada porque ninguém tinha resolvido um problema destes antes. Prognósticos, como dizia um grande pensador, só no fim do jogo.
Como quase tudo na vida, ver o mundo pelos olhos dos outros resolve muita coisa. Mesmo que esse outro seja um vírus.