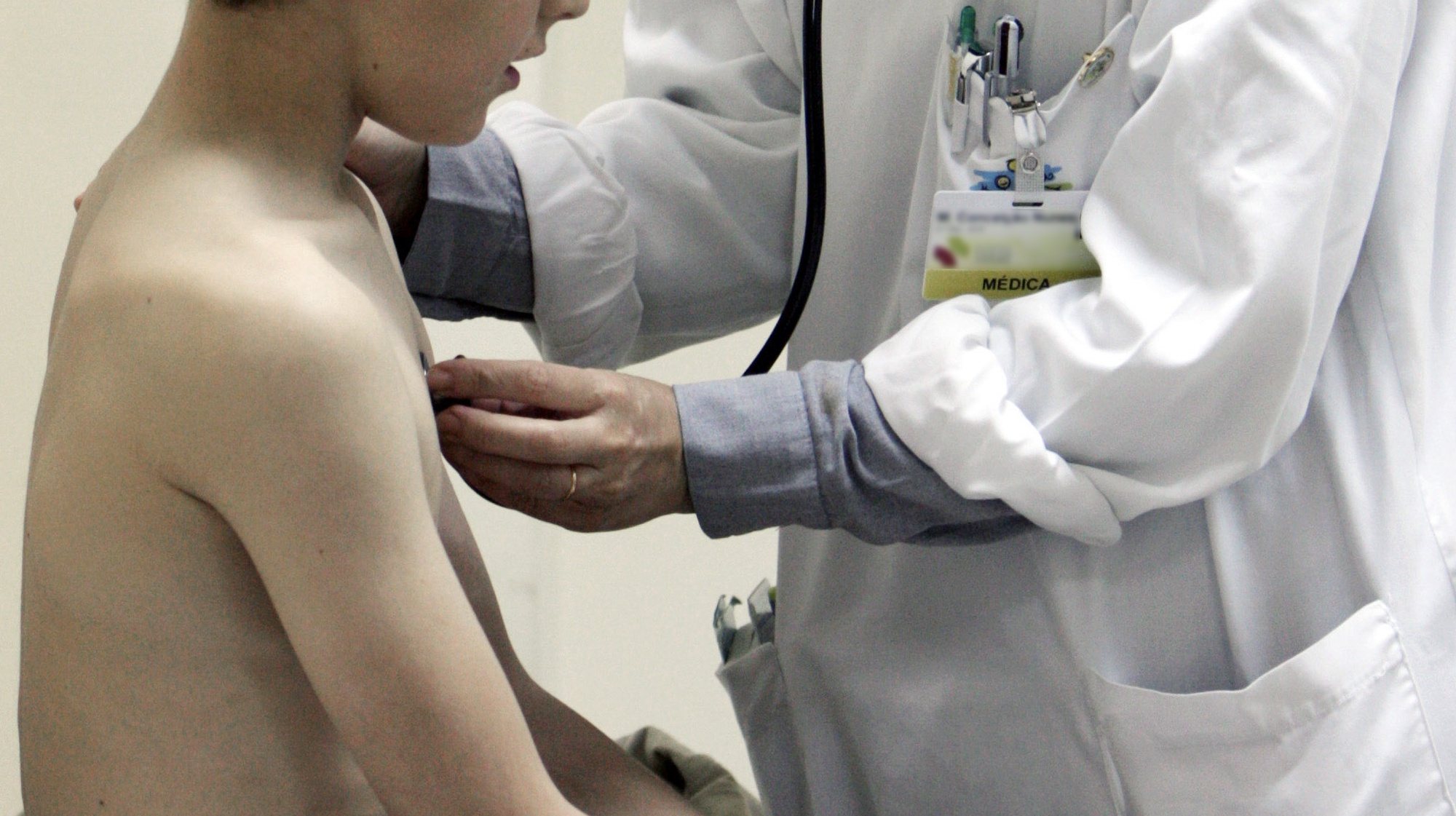
Há três semanas que Carlos Antunes, docente e investigador da Faculdade de Ciências da Universidade de Lisboa, sabia que chegaríamos por estes dias aos mil casos de infeção pelo novo coronavírus. As dezenas de folhas de Excel que tem preenchido desde o início da pandemia, umas quantas referentes a Portugal, outras tantas para o resto do mundo, o vão mantendo a par do que se passa no país e além fronteiras.
É um pouco como as previsões meteorológicas, compara o cientista em conversa com o Observador, mas com uma diferença fundamental: se um meteorologista lhe disser que vai chover dentro de três semanas, a margem de incerteza é muito elevada; mas, graças às fórmulas matemáticas que Carlos Antunes tem vindo a utilizar, o cientista tem conseguido prever com sucesso a evolução da Covid-19 em Portugal. E o seu conhecimento sobre o que se passa está muito mais à frente do que revelam os relatórios das autoridades de saúde.
Quando entrevistámos o professor da Universidade de Lisboa, Carlos Antunes ainda estava a terminar de preencher os dados publicados esta sexta-feira. Poucos minutos depois, já nos conseguia dizer o que nos reserva a segunda vaga se tudo continuar como está: 1.500 casos em média na próxima semana, 2.000 casos diários em novembro, uma pressão crescente no sistema de saúde e um pico indefinido, “a apontar para o céu”.

Carlos Antunes/FCUL/Universidade de Lisboa
O que se passou para termos chegado perto dos 1.500 casos diários no fim desta semana de outubro?
Os dados que nos são fornecidos publicamente não correspondem a infeções ocorridas no dia anterior: correspondem a resultados de testes cujas amostras podem ter sido recolhidas há uma semana e cujos sintomas podem ter ocorrido dez dias antes. A velocidade com que os dados são debitados enquanto resultados depende da própria eficiência e do ritmo do trabalho dos laboratórios que processam as amostras. Sabemos que há laboratórios que fecham ao fim de semana, por isso é que os números ao domingo e à segunda-feira são inferiores à média a meio da semana.
A essa variação chamamos ruído: são pequenos erros associados ao processo de aferição da medição dos números. Portanto, temos de pegar numa média móvel, que é a média dos sete dias, que é boa par suavizar a oscilação e que permite determinar a tendência — ou seja, quando uma curva indica que os casos estão a diminuir ou a subir. É essa a tendência para que olhamos. Isso permite-nos encontrar alterações a essa tendência, por exemplo, quando há medidas que impactam o contágio.
Ora, como nós tivemos um problema prolongado e houve um défice de casos reportados no domingo, segunda-feira e terça-feira [por causa do feriado de segunda], era expectável que, na quinta-feira, os números estivessem muito acima da média da tendência. Quando temos um número muito acima da tendência, chamamos uma anomalia positiva — temos casos reportados a mais — e quando está abaixo da média, temos uma anomalia negativa, ou seja, casos reportados a menos.
Dos números de quinta-feira, estava à espera. Só não esperava que fossem dois dias, quinta e sexta, muito acima da média. Agora é preciso olhar para os próximos dias e ver se esta tendência se continua a verificar, se de facto estes números são indicadores de um início de uma nova tendência. Os dados de sexta foram uma surpresa porque estava à espera de um valor na ordem dos mil casos, de acordo com o nosso modelo.
O sábado trouxe-nos 1.646 novos casos. Isso está dentro das suas previsões?
Sim, embora estejam acima da tendência de diagnóstico. Ou seja, em termos de número de contágio, estão dentro da estimativa; em termos de diagnóstico — que normalmente anda um pouco atrasado — estão acima da média, o que pode refletir um resultado de uma maior esforço de testagem e rastreio, isto é, uma maior eficácia das equipas que estão no terreno e maior capacidade de processamento de testes.
É expectável que nos próximos dias, em termos de notificação, os números baixem um pouco. Mas a partir de agora, depois desta tendência que ficou definida nesta semana, será de esperar que, em termos médios, os números semanais (a média da semana) comecem a ser sempre superiores a 1.500 casos diários.
O que é que isso nos diz em termos de propagação da doença?
Para sabermos isso precisamos de olhar para a data do início dos sintomas dos infetados, não para a data em que saiu o relatório do teste dessa pessoa. Os epidemiologistas ainda vão mais longe: pegam nesses dados e corrigem-nos em função do período de incubação do vírus. Essa é que é mesmo a curva epidémica, ou seja, é a curva da data de infeção. É extremamente difícil de calcular, mas o Instituto Ricardo Jorge fá-lo e chama-se nowcasting.
O especialista em biologia quer saber a propagação do contágio, não da doença, porque a ideia é tentar identificar quem está contagiado para evitar que um infetado contagie outras pessoas. Portanto, a ele não interessa o número de casos que são oficialmente reportados: o que interessa é o número de casos que hoje foi infetado. Funciona ao contrário: temos os casos reportados, vamos ao processo de cada caso ver quando foi o início dos sintomas e o caso salta para essa data. Se foi sete dias antes de o caso ser reportado, salta para sete dias antes. Isso, aliás, está nos relatórios da DGS [Direção-Geral da Saúde], na segunda página.
Como se faz isso tendo em conta que há muitos casos assintomáticos?
Se nós olharmos para esse gráfico, temos lá exatamente o número de casos confirmados por data de início dos sintomas, de diagnóstico ou de notificação. Há casos em que o médico não conseguiu identificar quando começaram os sintomas, como é o caso dos assintomáticos e, nesse caso, passa para a data da recolha da amostra. Se há dúvidas ou não se sabe quando é que foi colhida a amostra, passa para a data de notificação, ou seja, quando saiu o resultado.
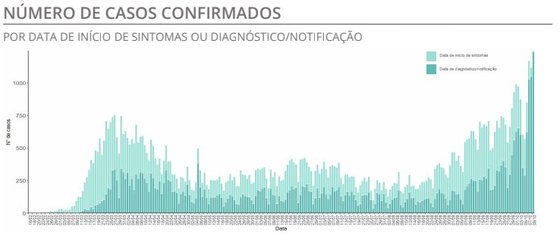
As barras do boletim a que o matemático se refere
É esse o significado daquelas barras azuis claras e azuis escuras [nos mapas diários da DGS]. As barras azuis escuras são os casos apontados na data de diagnóstico ou notificação; e as barras azuis claras são dos casos em que se sabe a data do início dos sintomas. O que os epidemiologistas fazem é corrigir ainda mais esses dados: aplicam uma distribuição que descreve, em função do período médio de incubação do vírus, o dia em que as pessoas foram contagiadas.
Mas o intervalo entre o dia do contágio e dos sintomas também pode variar de caso para caso.
O período médio de incubação é de cinco dias e também pode ir até aos catorze dias, mas isso é descrito por uma função matemática. Por isso, todos os dias correm um modelo matemático que distribui o número de casos para a data de contágio. E é com base nisso que eles calculam o R(t) [número de pessoas que cada pessoa contagia] que as autoridades de saúde divulgam nas conferências de imprensa. Só que, normalmente, esses cálculos vêm atrasados.
Então neste momento sabemos o R(t) de até que dia?
Agora está até dia 4 de outubro.
Porquê?
Porque esse método cria o chamado gap [em inglês, lacuna] na parte final. No final, esse gráfico cai e, portanto, não confiamos muito nesses dados finais, cortamos a série e fazemos apenas um cálculo de R(t) até aos três dias anteriores. Ou seja, normalmente, quando nos dizem que o R(t) está em 1,05, esse é, na verdade, o R(t) de há muitos dias antes. Entretanto tivemos uma evolução e provavelmente já está superior.
O que tenho feito é tentar otimizar este processo de nowcasting, em que vamos tentar descobrir quantos casos nós já identificámos e quantos casos já ocorreram, mas só vamos identificar daqui a uns dias. Sabendo esse período de incubação e sabendo como é que os sintomas se manifestam numa população, pegamos nessa distribuição — há fórmulas matemáticas para isso — e acrescentamos-lhe uma estimativa de casos que já foram infetados, mas que ainda não foram diagnosticados. É essa a curva que nos permite ver a tendência atual.
Sendo assim, qual é a realidade portuguesa neste momento?
Poderão estar a ser infetados atualmente cerca de 1.800 pessoas por dia, mas provavelmente só daqui a 15 dias é que esses casos vão ser identificados. Os casos reportados esta sexta-feira já deviam estar infetados há dez dias, alguns tiveram sintomas há cinco e só agora é que soubemos deles. Portanto, nós tentamos matematicamente estimar o que é que está a ocorrer agora em termos de contágio, senão andamos sempre atrasados.
É preciso identificar, dentro dos surtos e das cadeias de transmissão, as pessoas que tiveram contactos; recolher as amostras dessa pessoa, fazer os inquéritos epidemiológicos, ver qual é a probabilidade de estarem ou não infetadas, fazer a recolha das amostras… Depois há laboratórios que fazem o processo todo de testagem, outros que só fazem uma parte e enviam a amostra com o vírus inativo para outro laboratório. Só ao fim de quatro ou cinco dias é que temos o resultado.
E como estamos no que toca ao risco de transmissão?
Estamos com um R(t) de 1,15 neste momento. Desde 19 de agosto que o R(t) está acima de um, teve uma ligeira descida entre dia 15 e dia 20 de setembro, mas a abertura das escolas e o regresso à atividade de forma geral fez com que, a partir de dia 23 de setembro, ele voltasse a subir novamente.
Estimo valores mais altos que o Instituto Ricardo Jorge: no Norte um R(t) de 1,27; no Centro de 1,19; em Lisboa e Vale do Tejo estará em 1,05, mas continua em crescimento exponencial… As únicas regiões que estão com um R(t) abaixo de 1 é o Alentejo e o Algarve. Em termos de estimativa, a região Norte já ultrapassou o pico de março, a região Centro está a passar por ele. Lisboa teve um pico em setembro que foi superior ao de junho, mas está com um crescimento mais lento do que o da região Norte.
Como antevemos o número de contágios em cada dia, a curva permite-nos calcular o R(t) com mais rigor. Quando os valores do Instituto Ricardo Jorge são transmitidos nas conferências de imprensa, normalmente são valores que já calculei há uns dias.
E número de casos, pessoas contagiadas?
O que é que posso dizer sobre este momento?… Nós temos três curvas de incidências. Há uma que toda a gente consegue construir com o número de casos reportados diariamente, mas que não reflete a realidade do país, e que nos diz que, neste momento, temos uma média de 65 casos nos últimos sete dias por 100 mil habitantes. Lembra-se de falarem nos 20 casos por 100 mil habitantes e que esse seria, por assim dizer, um limiar?… Pois já vamos em 65 casos dos últimos sete dias por 100 mil habitantes.
Em termos médios, em termos de números de notificação, nós já atingimos os mil — portanto, já tivemos dois dias acima de mil e, fazendo a média dos últimos sete dias, já ficamos acima de mil. O que posso ver é que estamos a duplicar os casos a cada 28 a 30 dias. Tínhamos 500 casos no dia seis ou sete de setembro, agora esse número duplicou.
Então onde estaremos daqui a 30 dias?
Se olharmos para a série corrigida, em que tento estimar os casos que já foram infetados mas que só vão ser diagnosticados nos próximos dias, os cálculos dão-me dois mil casos diários de infeção do próximo mês. Esta é uma série mais fidedigna porque tem em conta o período de incubação da doença. Falou-se na comunicação social de quando é que nós iremos atingir os 1.500 casos e se isso era um ponto crítico… Provavelmente para a semana poderemos ter esses 1.500 casos. (entretanto ultrapassados já este sábado, com 1.696)
Também faço a mesma análise para os óbitos. A curva dos óbitos é muito mais estável, há três semanas já se verificava isso mesmo. Calculo o pico dos óbitos para dentro de quinze dias a um mês, com 20 óbitos diários. E até podemos ultrapassar esse valor porque a curva já ganhou inércia. Isso é preocupante porque significa que vai haver pressão nos internamentos e nos cuidados intensivos, como já se tem verificado. O número de óbitos respondem com um atraso de 21 dias: os casos começaram a subir em 19 de agosto, mas o número de mortes só começou a subir a 7 ou 8 de setembro. Só podemos esperar é que o país esteja preparado.
E o pico da epidemia?
Desenvolvi uma técnica para conseguir determinar o pico que se demonstrou boa para a primeira fase. Era baseada na taxa diária mas, neste momento, a taxa diária anda próxima de zero porque estamos a comparar o número de casos diários com o número total. Agora utilizo uma técnica em que pego na curva do R(t) e vou buscar a tendência dessa curva — porque basicamente sei, graças a um processo matemático, quando a propagação começa a desacelerar e converge para 1.
Então, o tal efeito de diminuição do R(t) até 23 de setembro indicava o pico para finais de outubro. Depois a tendência começou a inverter e começou a atirar o pico para meados de novembro. Agora o período é tão incerto e tão largo que há uma grande incerteza: pode ser desde meados de novembro até finais de dezembro. Isto tendo em conta os dados atuais, porque como o R(t) vai evoluir, o que isto vai significar é que o pico vai-se dar no infinito — ou seja, ficamos sem saber quando é que se vai dar, deixou de estar definido.
Sabe aquela curva que parece um sino? Chama-se curva gaussiana. Essa curva tem um crescimento exponencial, depois alcança um ponto de inflexão em que começa a dobrar, até começar a baixar. Isso acontece quando o R(t) converge para 1. O que estou a verificar agora é que ela deixou de existir: a tendência está a apontar para o céu. Não consigo prever neste momento. Bastou estes dois últimos dias para criar esta indefinição.
O que significam os 65 casos nos últimos sete dias por 100 mil habitantes?
↓ Mostrar
↑ Esconder
Carlos Antunes refere-se às palavras da diretora-geral da saúde, Graça Freitas, que na conferência de imprensa de quarta-feira, garantiu que “não estamos num crescimento exponencial” da epidemia em Portugal porque “todos os concelhos estão abaixo de 20 casos por 100 mil habitantes”.
Há uma ressalva que quero fazer: a ministra tem afirmado várias vezes, talvez para apaziguar a opinião pública, que não estamos a ter um aumento exponencial. Mas isso é um erro crasso matematicamente: sempre que o R(t) é superior a 1 estamos numa evolução exponencial — temos é uma exponencial inicial lenta, ou seja, cresce muito lentamente. Em vez de duplicar de três em três dias como verificávamos em março, estamos a duplicar a cada 30 dias.
Basta estar ligeiramente acima de 1 para termos um crescimento exponencial, assim como, se estivermos abaixo de 1, mantemos uma redução que é exponencial. É por isso que nós estamos em crescimento exponencial desde 19 de agosto. Aliás, é expectável que dupliquemos os casos num mês, mas se houver um aumento nesta tendência e se o R(t) subir, esse período vai ser encurtado.
Temos capacidade para detetar todos esses casos?
Aqui há duas corridas: a da velocidade com que o vírus se está a propagar e a do sistema de testagem. Podemos até fazer 100 mil testes todos os dias, seja o que for: se o número de casos que identificarmos por cada dia for inferior ao número de contágios, estamos a perder a corrida — o vírus vai-se propagar mais depressa do que nós o detetamos.
Imaginemos que hoje ocorreram mil infeções e nós, daqui a cinco dias, só detetamos 800. Isso significa que estamos com um défice de 200 casos. Ora, se o R(t) for 1,1, os mil casos de hoje vão infetar 1.100. E se detetarmos menos do que o número de infeções que estão a ocorrer, estamos a perder a corrida e o vírus vai avançando muito mais rapidamente. Por isso é que, a dada altura, consigo identificar as cadeias de transmissão e encontro uma série de infetados em excesso. Foi o que aconteceu e o que justifica o aumento desta semana.
A meta basicamente é quando nós atingimos o pico e quando conseguimos ser mais rápidos do que o vírus, começamos a detetar casos mais rápido do que essa propagação. Aí é que a curva começa a diminuir. A estratégia deve ser tentarmos ser mais eficientes nos inquéritos epidemiológicos, no seguimento dos surtos e das cadeias de transmissão, sermos mais prudentes na nossa proteção, no nosso comportamento social e no distanciamento. Dessa forma, conseguimos reduzir a velocidade do vírus e acelerar a nossa capacidade de teste.
O primeiro-ministro previu estes casos na semana passada. Sabe a fonte dessa previsão?
Não sei. Penso que não terão sido os meus cálculos porque eu há 15 dias já previa que chegaríamos aos mil casos notificados só no início de outubro. Mas pode ter sido intuitivo, talvez tenha olhado para os outros países e tido a percepção que, aquilo que está a acontecer na Holanda ou na República Checa, iria acontecer aqui. Portanto, isso era intuitivo desse ponto de vista. Não era preciso grande análise matemática — porque nós não tínhamos tomado medidas significativamente drásticas para que a nossa propagação não se desse à mesma taxa que nos outros países.
Mas porquê este atraso de uma semana?
Tem a ver com esse atraso de diagnóstico da efetiva transmissão. Portanto, há aqui uma incerteza nos próprios modelos matemáticos. E estes modelos não têm nada a ver com os modelos de matemática biológica que tentam prever a propagação de longo prazo. Este é um método de previsão de curto a médio prazo — quinze dias, três semanas — ou seja, são assertivos.
O que é importante nesta análise é que, quando a epidemia ganha o que nós chamamos em física de momento, quantidade de movimento, ela não altera o seu seu rumo, não altera o seu caminho… Se temos um camião a uma determinada velocidade, é preciso uma força maior do que a dele para o desviar do caminho. Aqui é a mesma coisa: a curva agora tem uma inércia, uma resistência à mudança, portanto, a epidemia já está mais extensa.
Que força maior a podia alterar, então?
Para mudar tinha de acontecer uma de duas coisas: ou uma mutação global do vírus e ele deixar de ser infeccioso; ou os hospedeiros mudarem o seu comportamento — isolarmo-nos, reduzirmos o contacto e a exposição. É a única forma de se inverter esta inércia. E mesmo assim é difícil: a subida no aumento de casos devido ao contágio ganhou inércia, ganhou velocidade, e agora torna-se cada vez mais difícil de parar. Portanto, o país e as entidades oficiais vão ter que repensar.
Talvez os modelos epidemiológicos matemáticos, se se introduzirem regras de restrição do contacto, funcionem… imaginemos que agora tomamos a uma decisão a nível nacional de confinamento ou cordões sanitários em determinadas regionais. Se fizermos isso, poderemos conter determinados surtos. E dessa poderá acontecer uma inversão do R(t) e a curva começa novamente a aproximar-se do tal achatamento.